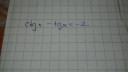Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segítenétek a Szögfüggvényben? SOS
 Mrs.Park
kérdése
Mrs.Park
kérdése
452
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Tudjuk, hogy ctg(x)=1/tg(x), tehát átírható így az egyenlet:
1/tg(x) - tg(x) = -2, a jobb átláthatóság kedvéért legyen tg(x)=z:
1/z - z = -2, szorzunk z-vel:
1 - z² = -2z, redukáljuk a bal oldalt 0-ra:
0=z²-2z-1, ennek a megoldásai:
z₁=(2+√8)/2=1+√2
z₂=(2-√8)/2=1-√2. Mivel z=tg(x) volt, ezért
tg(x)=1+√2, ezt visszakeressük számológéppel, ekkor a megoldások:
x=amit kiadott a számológép + k*π, ahol k tetszőleges egész, és
tg(x)=1-√2, ennek a megoldása x=amit kiadott a számológép + k*π, ahol k tetszőleges egész.
A számológépet ne felejtsd el RAD-ba váltani.
Egyébként nem lehet, hogy elírtad, és az eredeti egyenlet ctg(x)+tg(x)=-2?
1/tg(x) - tg(x) = -2, a jobb átláthatóság kedvéért legyen tg(x)=z:
1/z - z = -2, szorzunk z-vel:
1 - z² = -2z, redukáljuk a bal oldalt 0-ra:
0=z²-2z-1, ennek a megoldásai:
z₁=(2+√8)/2=1+√2
z₂=(2-√8)/2=1-√2. Mivel z=tg(x) volt, ezért
tg(x)=1+√2, ezt visszakeressük számológéppel, ekkor a megoldások:
x=amit kiadott a számológép + k*π, ahol k tetszőleges egész, és
tg(x)=1-√2, ennek a megoldása x=amit kiadott a számológép + k*π, ahol k tetszőleges egész.
A számológépet ne felejtsd el RAD-ba váltani.
Egyébként nem lehet, hogy elírtad, és az eredeti egyenlet ctg(x)+tg(x)=-2?
0
-
Mrs.Park: De meglehet... 8 éve 0
 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Csak azért kérdeztem, mert annak a megoldása sokkal szebb;
1/tg(x) + tg(x) = -2, a jobb átláthatóság kedvéért legyen tg(x)=z:
1/z + z = -2, szorzunk z-vel:
1 + z² = -2z, redukáljuk a jobb oldalt 0-ra:
z²+2z+1=0, ezt meg lehet oldani megoldóképlettel is, de ha teljes négyzetté alakítunk:
(z+1)²=0, ennek a megoldása z=-1, és mivel z=tg(x), ezért tg(x)=-1, ennek a megoldása x=-π/4 + k*π, ahol k tetszőleges egész.
1/tg(x) + tg(x) = -2, a jobb átláthatóság kedvéért legyen tg(x)=z:
1/z + z = -2, szorzunk z-vel:
1 + z² = -2z, redukáljuk a jobb oldalt 0-ra:
z²+2z+1=0, ezt meg lehet oldani megoldóképlettel is, de ha teljes négyzetté alakítunk:
(z+1)²=0, ennek a megoldása z=-1, és mivel z=tg(x), ezért tg(x)=-1, ennek a megoldása x=-π/4 + k*π, ahol k tetszőleges egész.
0
- Még nem érkezett komment!