Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Dinamika
 Attila089
kérdése
Attila089
kérdése
426
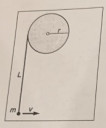
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Fizika
Válaszok
2 bongolo
{
bongolo
{  }
válasza
}
válasza
Most csak elkezdeni van időm:
Mivel nincs súrlódás, végig azonos marad a rendszer energiája, vagyis végig ugyanakkora `v` sebességgel mozog a test (amíg bele nem ütközik a hengerbe). Közben a fonal rátekeredik a hengerre. A test sebessége mindig a fonal pillanatnyi irányára merőleges lesz! Ehhez (mármint hogy megváltozzon a sebesség iránya) erő kell, ez pedig éppen az aktuális centripetális erő, `m·v^2/R`, ahol a nagy `R` a fonal aktuális (megrövidült) hossza. Ugyanis a test minden egyes pillanatban körmozgást végez azon pont, mint középpont körül, ami a fonalnak a pillanatnyi "utolsó" érintkezési pontja a hengerrel. Tehát nem a henger középpontja körül van a körmozgás!
Ez a centripetális erő nem végez munkát, mert az erő fonal irányú, a pillanatnyi elmozdulás (pillanatnyi sebesség) pedig arra merőleges. Ezért van, hogy a `v` sebesség állandó marad.
Majd este folytatom, ha addig nem találnád ki...
Mivel nincs súrlódás, végig azonos marad a rendszer energiája, vagyis végig ugyanakkora `v` sebességgel mozog a test (amíg bele nem ütközik a hengerbe). Közben a fonal rátekeredik a hengerre. A test sebessége mindig a fonal pillanatnyi irányára merőleges lesz! Ehhez (mármint hogy megváltozzon a sebesség iránya) erő kell, ez pedig éppen az aktuális centripetális erő, `m·v^2/R`, ahol a nagy `R` a fonal aktuális (megrövidült) hossza. Ugyanis a test minden egyes pillanatban körmozgást végez azon pont, mint középpont körül, ami a fonalnak a pillanatnyi "utolsó" érintkezési pontja a hengerrel. Tehát nem a henger középpontja körül van a körmozgás!
Ez a centripetális erő nem végez munkát, mert az erő fonal irányú, a pillanatnyi elmozdulás (pillanatnyi sebesség) pedig arra merőleges. Ezért van, hogy a `v` sebesség állandó marad.
Majd este folytatom, ha addig nem találnád ki...
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
A folytatás:
Ha tudnánk a test pályáját, illetve a pálya `s` hosszát, akkor -- mivel végig állandó `v` sebességgel megy a tárgy -- már meglenne, hogy `t=s/v` idő múlva csapódik be.
Persze igaziból a pálya alakja nem is kell, csak a hossza. Azt meg így lehet kiszámolni:
Legyen a fonal lelógó részének a pillanatnyi hossza `x`. (Ezt fentebb még `R`-rel jelöltem, a tanár meg `ℓ`-lel jelölte egyébként.) Kezdetben `x=L`, a végén `x=0`.
Először kell még egy kevés mese:
Egy kis `dt` idő alatt a test megtesz
`ds=v·dt`
hosszat a pályából. Ilyen rövid távon ez még a pillanatnyi forgás-középpont (ami a fonal és a henger utolsó érintkezési pontja) körüli elfordulást jelent, aminek sugara éppen `x`. Ezért a `ds` hossz a szögelfordulással így fejezhető ki: `ds=x·dφ`, vagyis
`dφ=(ds)/x`
Ennyit fordul el a fonal, közben egy pici része rátekeredik a hengerre. Hol lesz most, a rátekeredés után, a pillanatnyi utolsó érintkezési pont? Mármint az `r` sugarú hengeren mekkora szöggel odébb? Ez is éppen ugyanaz a `dφ`, hisz most is merőleges a fonal az új, elfordult `r` sugárra (érintő marad végig).
Mennyi fonál tekeredett fel az `r` sugarú hengerre? Egyszerű: `r·dφ`
Pont ennyivel csökken a fonal fel nem tekeredett (lelógó) hossza:
`dx=-r·dφ`
Azért negatív, mert csökken a hossz!
Ennyi volt a mese, most már csak írni kell a matekot:
Ebbe behelyettesítve `dφ` értékét:
`dx=-r·(ds)/x`
Amiből `ds`:
`ds=-x/r·dx`
Ha ezeket a kis `ds` darabokat öszeadogatjuk (magyarul összeintegráljuk), akkor megkapjuk a pálya teljes `s` hosszát:
`s=int_L^0 -x/r\ dx = [-x^2/(2r)]_L^0=L^2/(2r)`
Már kész is vagyunk az a)-val, hisz `t=s/v=L^2/(2rv)` simán kiszámolható.
b)
Kellene az `x(t)` függvény, hisz azt már az első válaszban írtam, hogy a centripetális erő `F(t)=m·v^2/(x(t))`
Fentebb már megvannak, hogy `dx=-r/x·ds` és `ds=v·dt`, vagyis
`dx=-r/x·v·dt`
`x·dx=-rv·dt`
Az a helyzet, hogy ez egy differenciálegyenlet, nem tudom, tanultok-e olyat a gimitekben. A megoldása ennek nem túl bonyolult: ha összeadogatnánk (integrálnánk) mind a két oldalt, mivel amiket az integrálás során öszeadogatunk a két oldalon, azok egyformák, az integrál eredménye is egyforma lesz:
`int\ x\ dx=int -rv\ dt`
A jobb oldal `t` szerinti integrál.
A bal oldalon `x` függ a `t`-től is, (szóval `x(t)`), de ez most nem számít, mert a bal oldal `x` szerinti integrál:
(Ez most határozatlan integrál, majd a peremfeltételekből jön ki a határozott megoldás.)
`x^2/2+C_1 = -rvt+C_2`
A két konstans végülis összevonható egy harmadikba:
`x^2/2 = C-rvt`
`x(t)=sqrt(2(C-rvt))`
(Pozitív kell legyen, mert a fizikai hossz nem lesz negatív, ezért a másodfokú egyenlet két gyökéből csak a pozitív maradt.)
Nem tudjuk, mennyi a `C`; az integrálásból csak annyit tudunk, hogy bármi lehet, szóval ez még nem a végleges megoldás.
Most jön a szerepe a peremfeltételnek: `t=0` időpontban `x=L`:
`x(0)=sqrt(2C)=L`
vagyis `C=L^2/2`
`x(t)=sqrt(L^2-2rvt)`
Ellenőrzés: a végén, vagyis `t=L^2/(2rv)` időpontban (ami fentebb az a) résznél jött ki) tényleg nulla-e a hossz? Rögtön látszik, hogy igen.
Ebből már az erő is simán felírható.
Ha tudnánk a test pályáját, illetve a pálya `s` hosszát, akkor -- mivel végig állandó `v` sebességgel megy a tárgy -- már meglenne, hogy `t=s/v` idő múlva csapódik be.
Persze igaziból a pálya alakja nem is kell, csak a hossza. Azt meg így lehet kiszámolni:
Legyen a fonal lelógó részének a pillanatnyi hossza `x`. (Ezt fentebb még `R`-rel jelöltem, a tanár meg `ℓ`-lel jelölte egyébként.) Kezdetben `x=L`, a végén `x=0`.
Először kell még egy kevés mese:
Egy kis `dt` idő alatt a test megtesz
`ds=v·dt`
hosszat a pályából. Ilyen rövid távon ez még a pillanatnyi forgás-középpont (ami a fonal és a henger utolsó érintkezési pontja) körüli elfordulást jelent, aminek sugara éppen `x`. Ezért a `ds` hossz a szögelfordulással így fejezhető ki: `ds=x·dφ`, vagyis
`dφ=(ds)/x`
Ennyit fordul el a fonal, közben egy pici része rátekeredik a hengerre. Hol lesz most, a rátekeredés után, a pillanatnyi utolsó érintkezési pont? Mármint az `r` sugarú hengeren mekkora szöggel odébb? Ez is éppen ugyanaz a `dφ`, hisz most is merőleges a fonal az új, elfordult `r` sugárra (érintő marad végig).
Mennyi fonál tekeredett fel az `r` sugarú hengerre? Egyszerű: `r·dφ`
Pont ennyivel csökken a fonal fel nem tekeredett (lelógó) hossza:
`dx=-r·dφ`
Azért negatív, mert csökken a hossz!
Ennyi volt a mese, most már csak írni kell a matekot:
Ebbe behelyettesítve `dφ` értékét:
`dx=-r·(ds)/x`
Amiből `ds`:
`ds=-x/r·dx`
Ha ezeket a kis `ds` darabokat öszeadogatjuk (magyarul összeintegráljuk), akkor megkapjuk a pálya teljes `s` hosszát:
`s=int_L^0 -x/r\ dx = [-x^2/(2r)]_L^0=L^2/(2r)`
Már kész is vagyunk az a)-val, hisz `t=s/v=L^2/(2rv)` simán kiszámolható.
b)
Kellene az `x(t)` függvény, hisz azt már az első válaszban írtam, hogy a centripetális erő `F(t)=m·v^2/(x(t))`
Fentebb már megvannak, hogy `dx=-r/x·ds` és `ds=v·dt`, vagyis
`dx=-r/x·v·dt`
`x·dx=-rv·dt`
Az a helyzet, hogy ez egy differenciálegyenlet, nem tudom, tanultok-e olyat a gimitekben. A megoldása ennek nem túl bonyolult: ha összeadogatnánk (integrálnánk) mind a két oldalt, mivel amiket az integrálás során öszeadogatunk a két oldalon, azok egyformák, az integrál eredménye is egyforma lesz:
`int\ x\ dx=int -rv\ dt`
A jobb oldal `t` szerinti integrál.
A bal oldalon `x` függ a `t`-től is, (szóval `x(t)`), de ez most nem számít, mert a bal oldal `x` szerinti integrál:
(Ez most határozatlan integrál, majd a peremfeltételekből jön ki a határozott megoldás.)
`x^2/2+C_1 = -rvt+C_2`
A két konstans végülis összevonható egy harmadikba:
`x^2/2 = C-rvt`
`x(t)=sqrt(2(C-rvt))`
(Pozitív kell legyen, mert a fizikai hossz nem lesz negatív, ezért a másodfokú egyenlet két gyökéből csak a pozitív maradt.)
Nem tudjuk, mennyi a `C`; az integrálásból csak annyit tudunk, hogy bármi lehet, szóval ez még nem a végleges megoldás.
Most jön a szerepe a peremfeltételnek: `t=0` időpontban `x=L`:
`x(0)=sqrt(2C)=L`
vagyis `C=L^2/2`
`x(t)=sqrt(L^2-2rvt)`
Ellenőrzés: a végén, vagyis `t=L^2/(2rv)` időpontban (ami fentebb az a) résznél jött ki) tényleg nulla-e a hossz? Rögtön látszik, hogy igen.
Ebből már az erő is simán felírható.
0
- Még nem érkezett komment!