Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Térfogat
 szg.k9kristof
{ Fortélyos } kérdése
szg.k9kristof
{ Fortélyos } kérdése
1423
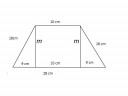
Mekkora a térfogata azoknak a 10 cm magas hasáboknak, amelyek felülnézete az ábrán látható?
Jelenleg 1 felhasználó nézi ezt a kérdést.
TK.180/4
TK.180/4
0
Általános iskola / Matematika
Válaszok
2 Voldemort
{ Elismert }
válasza
Voldemort
{ Elismert }
válasza
Szerintem a B.) megközelitőleg 5700 köbcm, mert a trapéz magassága nem egész szám
0
- Még nem érkezett komment!
 Janyta
megoldása
Janyta
megoldása
Hasáb térfogata = alapterület * testmagasság
B) trapéz alapú hasáb
alapterület = (a+c)*m /2
a magasságot Pitagorasz-tételével ki tudod számolni a magasság berajzolásával keletkező derékszögű háromszögből (csatolt ábra)
m²+9²=18²
m² = 243
m ∼ 15,59cm
Talap = (a+c)*m /2 = (28+10)*15,59/2 = 296,18 cm²
V = Talap *M = 296,18*10 = 2961,8 cm³
C) deltoid alapú hasáb
alapterület = e*f /2
Az e átlót a Pitagorasz-tételével ki tudod számolni, mivel a szomszédos 6cm-es oldalak derékszöget zárnak be:
e² = 6²+6² = 72
e = 8,48 cm
Az f (szimmetria)átlót szintén ki tudod számolni, mert az átlók merőlegesek egymásra, illetve a szimmetriaátló (f) felezi a másik átlót (e)
A szimmetriaátlót számoljuk ki két részletben: f = x+y
x²+(e/2)² = 6²
x²+4,24² = 6²
x² = 36-18 =18
x = 4,24
y²+(e/2)² = 8²
y²+4,24² = 8²
y² = 64-18 =46
y² = 6,78
f = x+y = 4,24+6,78 = 11,02cm
Talap = e*f /2 = 8,48*11,02/2 = 46,72cm²
V = Talap *M = 46,72*10 = 467,2 cm³
C) rombusz alapú hasáb
alapterület = e*f /2
A rövidebb átló (e) szintén 7 cm, mert az oldalak által bezárt hegyeszög 60°.
A másik átlót (f) Pitagorasz-tételével ki tudod számolni, mivel az átlók merőlegesen felezik egymást:
(f/2)²+3,5²=7²
(f/2)² = 36,75
f/2 = 6,06
f = 12,12cn
Talap = e*f /2 = 7*12,12/2 = 42,43cm²
V = Talap *M = 42,43*10 = 424,3 cm³
B) trapéz alapú hasáb
alapterület = (a+c)*m /2
a magasságot Pitagorasz-tételével ki tudod számolni a magasság berajzolásával keletkező derékszögű háromszögből (csatolt ábra)
m²+9²=18²
m² = 243
m ∼ 15,59cm
Talap = (a+c)*m /2 = (28+10)*15,59/2 = 296,18 cm²
V = Talap *M = 296,18*10 = 2961,8 cm³
C) deltoid alapú hasáb
alapterület = e*f /2
Az e átlót a Pitagorasz-tételével ki tudod számolni, mivel a szomszédos 6cm-es oldalak derékszöget zárnak be:
e² = 6²+6² = 72
e = 8,48 cm
Az f (szimmetria)átlót szintén ki tudod számolni, mert az átlók merőlegesek egymásra, illetve a szimmetriaátló (f) felezi a másik átlót (e)
A szimmetriaátlót számoljuk ki két részletben: f = x+y
x²+(e/2)² = 6²
x²+4,24² = 6²
x² = 36-18 =18
x = 4,24
y²+(e/2)² = 8²
y²+4,24² = 8²
y² = 64-18 =46
y² = 6,78
f = x+y = 4,24+6,78 = 11,02cm
Talap = e*f /2 = 8,48*11,02/2 = 46,72cm²
V = Talap *M = 46,72*10 = 467,2 cm³
C) rombusz alapú hasáb
alapterület = e*f /2
A rövidebb átló (e) szintén 7 cm, mert az oldalak által bezárt hegyeszög 60°.
A másik átlót (f) Pitagorasz-tételével ki tudod számolni, mivel az átlók merőlegesen felezik egymást:
(f/2)²+3,5²=7²
(f/2)² = 36,75
f/2 = 6,06
f = 12,12cn
Talap = e*f /2 = 7*12,12/2 = 42,43cm²
V = Talap *M = 42,43*10 = 424,3 cm³
1
- Még nem érkezett komment!