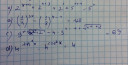Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
 dora-nagy3141
kérdése
dora-nagy3141
kérdése
593
Sziasztok! Valaki tud egy kicsit segíteni?

Jelenleg 1 felhasználó nézi ezt a kérdést.
exponenciális, egyenletek, dolgozat, sos, házi, házi
exponenciális, egyenletek, dolgozat, sos, házi, házi
0
Középiskola / Matematika
Válaszok
1 Rantnad
{
Rantnad
{  }
válasza
}
válasza
a) Használjuk a hatványozás azonosságait:
2⁴*2x+2³*2x+2x=5*5x-5x, elvégezzük a hatványozásokat:
16*2x+8*2x+2x=5*5x-5x, összevonunk mindkét oldalon:
25*2x=4*5x, osztunk 4-gyel és 2x-nel:
25/4=5x/2x, használjuk újból az azonosságokat:
(5/2)²=(5/2)x, ennek az exponenciális függvény szigorú monotonitása miatt akkor lesznek egyenlők, hogyha a kitevők egyenlők, tehát 2=x esetén.
b) (1/4)³=1/64=(1/8)², tehát ez lesz az egyenlet:
(1/8)2x-(1/8)x-1=128, azonosság:
((1/8)x)²-(1/8)x/(1/8)=128, ha (1/8)x=z, akkor
z²-z/(1/8)=128, az osztó tört reciprokával szorzunk:
z²-8z=128, 0-ra redukálunk:
z²-8z-128=0, ennek a megoldásai z₁=16, z₂=-8, tehát
(1/8)x=z, vagyis
(1/8)x=16, a közös alap a 2 lesz:
2-3x=2⁴, erre -3x=4, vagyis x=-4/3
(1/8)x=z, vagyis
(1/8)x=-8, ennek pedig nem lesz megoldása, mivel egy pozitív szám minden hatványa pozitív.
c) Ez elsőre rondának néz ki, de észrevehető, hogy mindkét kitevőben van x+√ x²+2 , így ezt lecseréljük; x+√ x²+2 =z, ekkor:
9z-4*3z-1=69, használjuk a hatványozás azonosságait:
(3z)²-(4/3)*3z=69, újabb ismeretlen: 3z=s, így
s²-(4/3)s=69, rendezzük az egyenletet:
s²-(4/3)s-69=0, esetleg lehet szorozni 3-mal:
3s²-4s-207=0, ennek a megoldásai: s₁=9, s₂=-23/3, tehát
3z=s → 3z=9 → z=2 (szig mon blabla)
3z=s → 3z=-23/3, ennek nincs megoldása
x+√ x²+2 =z → x+√ x²+2 =2, kivonunk x-et:
√ x²+2 =2-x, erre kikötést írunk; egyrészt a gyökjel alatt nem állhat negatív szám, tehát x²+2≥0,vagyis x²≥-2, ez minden x-re teljesül, mivel minden szám négyzete pozitív vagy 0, ezek mind nagyobbak -2-nél, másfelől a bal oldal értéke legalább 0, így a jobb oldal értéke is: 2-x≥0, tehát 2≥x. Ezután négyzetre tudunk emelni:
x²+2=4-4x+x², rendezés után 1/2=x-et kapjuk, ami beleesik az értelmezési tartományba.
d) Hatványozás azonosságai szerint összevonjuk:
4sin²(x)+cos²(x)=4, az exponenciális függvény szigorú monotonitása miatt...:
sin²(x)+cos²(x)=1, ez pedig egy alapvető trigonometrikus azonosság, tehát minden x-re igaz lesz.
Ha valami nem világos, kérdezz!
2⁴*2x+2³*2x+2x=5*5x-5x, elvégezzük a hatványozásokat:
16*2x+8*2x+2x=5*5x-5x, összevonunk mindkét oldalon:
25*2x=4*5x, osztunk 4-gyel és 2x-nel:
25/4=5x/2x, használjuk újból az azonosságokat:
(5/2)²=(5/2)x, ennek az exponenciális függvény szigorú monotonitása miatt akkor lesznek egyenlők, hogyha a kitevők egyenlők, tehát 2=x esetén.
b) (1/4)³=1/64=(1/8)², tehát ez lesz az egyenlet:
(1/8)2x-(1/8)x-1=128, azonosság:
((1/8)x)²-(1/8)x/(1/8)=128, ha (1/8)x=z, akkor
z²-z/(1/8)=128, az osztó tört reciprokával szorzunk:
z²-8z=128, 0-ra redukálunk:
z²-8z-128=0, ennek a megoldásai z₁=16, z₂=-8, tehát
(1/8)x=z, vagyis
(1/8)x=16, a közös alap a 2 lesz:
2-3x=2⁴, erre -3x=4, vagyis x=-4/3
(1/8)x=z, vagyis
(1/8)x=-8, ennek pedig nem lesz megoldása, mivel egy pozitív szám minden hatványa pozitív.
c) Ez elsőre rondának néz ki, de észrevehető, hogy mindkét kitevőben van x+√ x²+2 , így ezt lecseréljük; x+√ x²+2 =z, ekkor:
9z-4*3z-1=69, használjuk a hatványozás azonosságait:
(3z)²-(4/3)*3z=69, újabb ismeretlen: 3z=s, így
s²-(4/3)s=69, rendezzük az egyenletet:
s²-(4/3)s-69=0, esetleg lehet szorozni 3-mal:
3s²-4s-207=0, ennek a megoldásai: s₁=9, s₂=-23/3, tehát
3z=s → 3z=9 → z=2 (szig mon blabla)
3z=s → 3z=-23/3, ennek nincs megoldása
x+√ x²+2 =z → x+√ x²+2 =2, kivonunk x-et:
√ x²+2 =2-x, erre kikötést írunk; egyrészt a gyökjel alatt nem állhat negatív szám, tehát x²+2≥0,vagyis x²≥-2, ez minden x-re teljesül, mivel minden szám négyzete pozitív vagy 0, ezek mind nagyobbak -2-nél, másfelől a bal oldal értéke legalább 0, így a jobb oldal értéke is: 2-x≥0, tehát 2≥x. Ezután négyzetre tudunk emelni:
x²+2=4-4x+x², rendezés után 1/2=x-et kapjuk, ami beleesik az értelmezési tartományba.
d) Hatványozás azonosságai szerint összevonjuk:
4sin²(x)+cos²(x)=4, az exponenciális függvény szigorú monotonitása miatt...:
sin²(x)+cos²(x)=1, ez pedig egy alapvető trigonometrikus azonosság, tehát minden x-re igaz lesz.
Ha valami nem világos, kérdezz!
0
- Még nem érkezett komment!