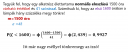Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valószínűségszámítás
 zoli0198
kérdése
zoli0198
kérdése
615
Tegyük fel, hogy egy alkatrész élettartama normális eloszlású 1500 óra várható értékkel és 41 szórással. Számítsuk ki, hogy az első 500 órában a lámpák hány százaléka megy tönkre!
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, valség, valószínűségszámítás
matek, valség, valószínűségszámítás
0
Felsőoktatás / Matematika
Válaszok
4 BGY
válasza
BGY
válasza
Grafikus kalkulátorral gyors
p( x kisebb 500 ) = 0
ha várh érték = 1500
szórás = 41
egyébként standardizálni kell és kell egy táblázat. BGY
p( x kisebb 500 ) = 0
ha várh érték = 1500
szórás = 41
egyébként standardizálni kell és kell egy táblázat. BGY
0
- Még nem érkezett komment!
 Törölt
{ Matematikus }
válasza
Törölt
{ Matematikus }
válasza
Csatoltam képet. Nem gondolom, hogy levezetés nélkül elfogadják a kalkulátor értékét. Már csak azért is, mert érezzük, hogy egy várhatóan 1500 órás élettartammal és kis szórással rendelkező valószínűségeloszlás bekövetkezési esélye gyakorlatilag zéró.
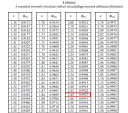
Táblázat:
https://math.bme.hu/~jmala/OKTATAS/A3/A3_2019-20_%C5%91sz/kepletek/standard_normalis_eloszlas.pdf
Magyarázat:
https://www.mateking.hu/valoszinusegszamitas/nevezetes-diszkret-es-folytonos-eloszlasok/exponencialis-normalis-es-egyenletes#79
Táblázat:
https://math.bme.hu/~jmala/OKTATAS/A3/A3_2019-20_%C5%91sz/kepletek/standard_normalis_eloszlas.pdf
Magyarázat:
https://www.mateking.hu/valoszinusegszamitas/nevezetes-diszkret-es-folytonos-eloszlasok/exponencialis-normalis-es-egyenletes#79
Módosítva: 5 éve
0
- Még nem érkezett komment!
 Törölt
{ Matematikus }
megoldása
Törölt
{ Matematikus }
megoldása
Csatoltam képet. Azért azt is érdemes megfigyelni, hogy Kolmogorov a biztos esemény valószínűségét tüntette fel 1-nek az axiómái közt, és mélyen hallgatott arról, hogy a lehetetlen esemény valszínje nulla, pedig ez igaz, de a baj ott kezdődik, hogy a fenti példa is azt mutatja, hogy bár a valszín nulla, még sincs arra garancia az, hogy az égőnk nem purcan ki 500 órán belül.
Módosítva: 5 éve
0
- Még nem érkezett komment!
 Törölt
{ Matematikus }
válasza
Törölt
{ Matematikus }
válasza
Csatoltam képet. Kérdésedre mutatok másik példát. OK?
Módosítva: 5 éve
0
- Még nem érkezett komment!