Question

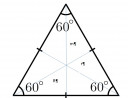
Egy szabályos ∆ kerülete 54 cm. Mekkora a ∆ területe, a ∆ köré és a ∆-be írható kör sugara?

daniella.danka { Kérdező } kérdése

498 5 éve

köré írható kör sugara: a.b.c/4.T
háromszögbe írható kör sugara: s.r ahol s=Kerület/2

Ezekkel számoltam, de nem jó értékek jöttek ki. Szerintem az elején rontottam el.
Valaki tud segíteni?

Jelenleg 1 felhasználó nézi ezt a kérdést.
pitagorasz, tétel, matek

0

Középiskola / Matematika

Válaszok

1

**ehavasi** megoldása · Accepted Answer · 2020-05-02 18:22:05

A szabályos háromszögről tudjuk, hogy a magasságvonalai és szögfelezői egybeesnek, metszéspontjuk és valamelyik csúcs távolsága a magasság kétharmada, a metszéspont és valamelyik magasságpont távolsága a magasság egyharmada.
A metszéspont egyben a körülírható és a beírható körnek is középpontja.
K=3·a ebből a=K/3=54/3=18 cm
A magasságvonalak két egybevágó háromszögre bontják a szabályos háromszöget, erre felírjuk a Pitagorasz tételt:
a²=(a/2)²+m² ebből m=15,59 cm
A beírható kör sugara r=m/3=5,2 cm
A körülírható kör sugara R=2·m/3=10,4 cm
A terület T=a·m/2=140,3 cm²

Keresés

Toplista

Egy szabályos ∆ kerülete 54 cm. Mekkora a ∆ területe, a ∆ köré és a ∆-be írható kör sugara?

Válaszok