Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segítségre lenne szükségem az alábbi elektrodinamika példában!
 LM96
kérdése
LM96
kérdése
882
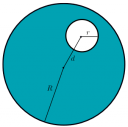
Az R sugarú, igen hosszú vezető hengerbe r sugarú, henger alakú vájatot vágunk. A két henger hossztengelyének távolsága d, úgy, hogy d<r és d+r<R. A vezetőben Z irányú, homogén j₀ sűrűségű áram folyik. Mi a mágneses indukció és a vektorpotenciál a vájatban?
Jelenleg 1 felhasználó nézi ezt a kérdést.
elektrodinamika, áramsűrűség, mágneses, indukció, vektorpotenciál, hengervájat, henger
elektrodinamika, áramsűrűség, mágneses, indukció, vektorpotenciál, hengervájat, henger
0
Felsőoktatás / Fizika
Válaszok
2 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Először ne törődjünk a vájattal, hanem számoljuk ki, hogy mi lenne a mágneses mező a vájat nélküli henger belsejében, a tengelytől `rho` távolságra. Ez a `\mathbf{H}_1` mező tisztán azimutális irányú, a nagyságának meghatározásához írjuk fel az Ampère-törvényt egy `rho` sugarú körre:
`oint \ \mathbf{H}_1 d\mathbf{l}=int \ \mathbf{J} d\mathbf{S}`
`H_{1 varphi}*2pi rho=J_0 * rho^2 pi`
`\mathbf{H}_1(rho)=1/2 J_0 rho \mathbf{e}_varphi`
Most nézzük meg, hogy milyen teret hozna létre a hengerből kivágott darab (tehát a kisebb, `r` sugarú henger) önmagában akkor, ha nem `J_0`, hanem `-J_0` áram folyna benne. Emögött az a ráció, hogy a Maxwell-egyenletek linearitása miatt használható a szuperpozíció elve, vagyis az eredő áramkép által keltett mágneses tér a két külön kiszámolt tér összege lesz. Az előbbihez hasonlóan, ha most a vájat közepébe tesszük a hengerkoordinátarendszer origóját, akkor ugyanolyan alakú lesz a tér:
`\mathbf{H}_2(rho^')=-1/2 J_0 rho^' \mathbf{e}_varphi^'`
A vesszős változók itt arra utalnak, hogy ezek egy másik, az előzőhöz képest eltolt hengerkoordinátarendszer irányait jelölik. Az eredő teret megkapjuk, ha `\mathbf{H}_1`-et és `\mathbf{H}_2`-t összeadjuk, de ehhez előbb egyeztetni kell a koordinátarendszereket. Helyezzük az elrendezést derékszögű koordinátarendszerbe úgy, hogy a nagy henger tengelye legyen a `z` tengely, a lyuk középpontja pedig essen az `x` tengelyre. A fenti terek ebben a közös koordinátarendszerben:
`\mathbf{H}_1``=``[[H_{1x}],[H_{1y}],[H_{1z}]]``=``[[1/2 J_0 rho cos varphi],[1/2 J_0 rho sin varphi],[0]]``=``[[1/2 J_0 sqrt(x^2+y^2)(-y)/sqrt(x^2+y^2)],[1/2 J_0 sqrt(x^2+y^2) x/sqrt(x^2+y^2)],[0]]``=``1/2 J_0 [[-y],[x],[0]]`
`\mathbf{H}_2``=``[[H_{2x}],[H_{2y}],[H_{2z}]]``=``[[-1/2 J_0 rho^' cos varphi^'],[-1/2 J_0 rho^' sin varphi^'],[0]]``=``[[-1/2 J_0 sqrt((x-d)^2+y^2)(-y)/sqrt((x-d)^2+y^2)],[-1/2 J_0 sqrt((x-d)^2+y^2) (x-d)/sqrt((x-d)^2+y^2)],[0]]``=``-1/2 J_0 [[-y],[x-d],[0]]`
Tehát az eredő tér a vájat belsejében:
`\mathbf{H}=\mathbf{H}_1+\mathbf{H}_2``=``[[0],[1/2 J_0 d],[0]]`
A látszólag nehéz feladatra nagyon egyszerű eredményt kaptunk: a vájatban homogén, `1/2 J_0 d` nagyságú mágneses tér alakul ki.
Akkor nézzük a vektorpotenciált:
`mu_0 \mathbf{H} = \text{rot} \ \mathbf{A}`
A vektorpotenciálnak csak tengelyirányú komponense van, és ebben az irányban az elrendezés eltolásinvariáns, vagyis `partial/(partial z)=0`. Ez a potenciál automatikusan teljesíti a Coulomb-mértéket (`\text{div} \ \mathbf{A}=0`), és jelentősen egyszerűsíti a rotáció képzését:
`\text{rot} \ \mathbf{A} ``=`` |(\mathbf{e}_x,\mathbf{e}_y,\mathbf{e}_z),(partial/(partial x),partial/(partial y),0),(0,0,A_z)|``=``[[(partial A_z)/(partial y)],[-(partial A_z)/(partial x)],[0]]`
Tehát `(partial A_z)/(partial x)=-1/2 mu_0 J_0 d` és `(partial A_z)/(partial y)=0`. Innen a vektorpotenciál:
`\mathbf{A}=(-1/2 mu_0 J_0 d x+C) \mathbf{e}_z`
`oint \ \mathbf{H}_1 d\mathbf{l}=int \ \mathbf{J} d\mathbf{S}`
`H_{1 varphi}*2pi rho=J_0 * rho^2 pi`
`\mathbf{H}_1(rho)=1/2 J_0 rho \mathbf{e}_varphi`
Most nézzük meg, hogy milyen teret hozna létre a hengerből kivágott darab (tehát a kisebb, `r` sugarú henger) önmagában akkor, ha nem `J_0`, hanem `-J_0` áram folyna benne. Emögött az a ráció, hogy a Maxwell-egyenletek linearitása miatt használható a szuperpozíció elve, vagyis az eredő áramkép által keltett mágneses tér a két külön kiszámolt tér összege lesz. Az előbbihez hasonlóan, ha most a vájat közepébe tesszük a hengerkoordinátarendszer origóját, akkor ugyanolyan alakú lesz a tér:
`\mathbf{H}_2(rho^')=-1/2 J_0 rho^' \mathbf{e}_varphi^'`
A vesszős változók itt arra utalnak, hogy ezek egy másik, az előzőhöz képest eltolt hengerkoordinátarendszer irányait jelölik. Az eredő teret megkapjuk, ha `\mathbf{H}_1`-et és `\mathbf{H}_2`-t összeadjuk, de ehhez előbb egyeztetni kell a koordinátarendszereket. Helyezzük az elrendezést derékszögű koordinátarendszerbe úgy, hogy a nagy henger tengelye legyen a `z` tengely, a lyuk középpontja pedig essen az `x` tengelyre. A fenti terek ebben a közös koordinátarendszerben:
`\mathbf{H}_1``=``[[H_{1x}],[H_{1y}],[H_{1z}]]``=``[[1/2 J_0 rho cos varphi],[1/2 J_0 rho sin varphi],[0]]``=``[[1/2 J_0 sqrt(x^2+y^2)(-y)/sqrt(x^2+y^2)],[1/2 J_0 sqrt(x^2+y^2) x/sqrt(x^2+y^2)],[0]]``=``1/2 J_0 [[-y],[x],[0]]`
`\mathbf{H}_2``=``[[H_{2x}],[H_{2y}],[H_{2z}]]``=``[[-1/2 J_0 rho^' cos varphi^'],[-1/2 J_0 rho^' sin varphi^'],[0]]``=``[[-1/2 J_0 sqrt((x-d)^2+y^2)(-y)/sqrt((x-d)^2+y^2)],[-1/2 J_0 sqrt((x-d)^2+y^2) (x-d)/sqrt((x-d)^2+y^2)],[0]]``=``-1/2 J_0 [[-y],[x-d],[0]]`
Tehát az eredő tér a vájat belsejében:
`\mathbf{H}=\mathbf{H}_1+\mathbf{H}_2``=``[[0],[1/2 J_0 d],[0]]`
A látszólag nehéz feladatra nagyon egyszerű eredményt kaptunk: a vájatban homogén, `1/2 J_0 d` nagyságú mágneses tér alakul ki.
Akkor nézzük a vektorpotenciált:
`mu_0 \mathbf{H} = \text{rot} \ \mathbf{A}`
A vektorpotenciálnak csak tengelyirányú komponense van, és ebben az irányban az elrendezés eltolásinvariáns, vagyis `partial/(partial z)=0`. Ez a potenciál automatikusan teljesíti a Coulomb-mértéket (`\text{div} \ \mathbf{A}=0`), és jelentősen egyszerűsíti a rotáció képzését:
`\text{rot} \ \mathbf{A} ``=`` |(\mathbf{e}_x,\mathbf{e}_y,\mathbf{e}_z),(partial/(partial x),partial/(partial y),0),(0,0,A_z)|``=``[[(partial A_z)/(partial y)],[-(partial A_z)/(partial x)],[0]]`
Tehát `(partial A_z)/(partial x)=-1/2 mu_0 J_0 d` és `(partial A_z)/(partial y)=0`. Innen a vektorpotenciál:
`\mathbf{A}=(-1/2 mu_0 J_0 d x+C) \mathbf{e}_z`
Módosítva: 5 éve
0
-
LM96: Nagyon köszönöm a segítséget!!!! 5 éve 0
 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
Egy plusz érdekesség: csináltam egy végeselemes szimulációt Comsol Multiphysics segítségével. A mellékelt ábrán a `\mathbf{B}` mező látható, színskálán a nagysága, nyilakkal az iránya. Látszik, hogy visszakaptuk az elméleti eredményt: az `x` tengelyre igazított vájatban homogén, `y` irányú a mező.
Egyismeretlenes, kétdimenziós peremérték-feladatként kellett megfogalmazni a problémát ahhoz, hogy a Comsol meg tudja oldani. Ehhez a vektorpotenciál definícióját (`\mathbf{H}=1/mu \text{rot} \ \mathbf{A}`) helyettesítsük be a differenciális Ampère-törvénybe (`\text{rot} \ \mathbf{H}=\mathbf{J}`), majd az így kapott egyenletben (`\text{rot} \ \text{rot} \ \mathbf{A}=mu \mathbf{J}`) használjuk ki az ismert `\text{rot} \ \text{rot} = \text{grad} \ \text{div} - Delta` azonosságot. Ha a Coulomb-mérték választásával élünk (`\text{div} \ \mathbf{A}=0`), akkor ezzel vektoriális Laplace–Poisson-egyenletet kapunk a vektorpotenciálra `(Delta \mathbf{A}=-mu \mathbf{J})`. Ez derékszögű koordinátarendszerben szétesik három skaláris LP-egyenletre, amiből nekünk csak a `z` irány érdekes: `Delta A_z = - mu J_0`. Ez alakilag ugyanolyan, mint az elektrosztatikában megismert, az elektromos skalárpotenciálra felírható egyenlet, numerikusan könnyen megoldható.
Egyismeretlenes, kétdimenziós peremérték-feladatként kellett megfogalmazni a problémát ahhoz, hogy a Comsol meg tudja oldani. Ehhez a vektorpotenciál definícióját (`\mathbf{H}=1/mu \text{rot} \ \mathbf{A}`) helyettesítsük be a differenciális Ampère-törvénybe (`\text{rot} \ \mathbf{H}=\mathbf{J}`), majd az így kapott egyenletben (`\text{rot} \ \text{rot} \ \mathbf{A}=mu \mathbf{J}`) használjuk ki az ismert `\text{rot} \ \text{rot} = \text{grad} \ \text{div} - Delta` azonosságot. Ha a Coulomb-mérték választásával élünk (`\text{div} \ \mathbf{A}=0`), akkor ezzel vektoriális Laplace–Poisson-egyenletet kapunk a vektorpotenciálra `(Delta \mathbf{A}=-mu \mathbf{J})`. Ez derékszögű koordinátarendszerben szétesik három skaláris LP-egyenletre, amiből nekünk csak a `z` irány érdekes: `Delta A_z = - mu J_0`. Ez alakilag ugyanolyan, mint az elektrosztatikában megismert, az elektromos skalárpotenciálra felírható egyenlet, numerikusan könnyen megoldható.
0
- Még nem érkezett komment!