Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Háromszög magasságának kiszámítása
bogáta
kérdése
17371
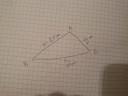
Adott egy háromszög, oldalai a=13 cm b=21 cm c=20 cm
Mekkora a C csúcshoz tartozó magassága?
Mekkora a C csúcshoz tartozó magassága?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2
Rantnad
{ 
}
válasza
Legyen a C csúcsnál lévő szög γ, ekkor a koszinusztétel:
21²=13²+20²-2*13*20*cos(γ)
441=169+400-520*cos(γ)
-128=-520*cos(γ)
16/65=cos(γ), itt kiszámolhatjuk a szöget, de a magasságra pontosabb értéket kapunk, ha ebből kiszámoljuk a szög szinuszát; ismerjük az alábbi összefüggést; sin²(γ)+cos²(y)=1, ide írjuk be cos(γ) értékét:
sin²(γ)+(16/65)²=1
sin²(γ)+256/4225=4225/4225
sin²(γ)=3969/4225
sin(γ)=√ 3969 /65.
A háromszög területe az egyik oldalról a*b*sin(γ)/2=20*23*√ 3969 /65/2=46*√ 3969 /13 cm², másfelől 21*m/2, ezek értelemszerűen egyenlőek:
46*√ 3969 /13=21*m/2, ezt kell megoldani m-re.
Ha valami nem érthető, várom kérdéseidet!
21²=13²+20²-2*13*20*cos(γ)
441=169+400-520*cos(γ)
-128=-520*cos(γ)
16/65=cos(γ), itt kiszámolhatjuk a szöget, de a magasságra pontosabb értéket kapunk, ha ebből kiszámoljuk a szög szinuszát; ismerjük az alábbi összefüggést; sin²(γ)+cos²(y)=1, ide írjuk be cos(γ) értékét:
sin²(γ)+(16/65)²=1
sin²(γ)+256/4225=4225/4225
sin²(γ)=3969/4225
sin(γ)=√ 3969 /65.
A háromszög területe az egyik oldalról a*b*sin(γ)/2=20*23*√ 3969 /65/2=46*√ 3969 /13 cm², másfelől 21*m/2, ezek értelemszerűen egyenlőek:
46*√ 3969 /13=21*m/2, ezt kell megoldani m-re.
Ha valami nem érthető, várom kérdéseidet!
0
-
bogáta: ami azt illeti, ilyesmiket még nem tanultunk(9.-es vagyok), és példának megcsináltuk azt, hogy az A csúcshoz tartozó magasság mennyi. azt pedig a következőképpen: ATC háromszög: m^2=13^2-x^2 BTA háromszög:m^2=20^2-(21-x)^2 ---> 13^2-x^2=20^2-(21-x)^2 7 éve 0
-
Rantnad: Akkor az oroszlánrésze megvan, csak az egyenletet kell megoldani. Az nem megy? 7 éve 0
-
bogáta: hát próbálgattam, de nagyon nem akart kijönni, mindig túl nagy értéket kaptam 7 éve 0
Rantnad
{ }
megoldása
13^2-x^2=20^2-(21-x)^2 | elvégezzük a négyzetre emeléseket
169-x²=400-441+42x-x² | összevonunk
169-x²=-41+42x-x² | +x²
169=-41+42x | +41
210=42x | :42
5=x, innen m²=13^2-5^2=144, erre m=12 adódik.
169-x²=400-441+42x-x² | összevonunk
169-x²=-41+42x-x² | +x²
169=-41+42x | +41
210=42x | :42
5=x, innen m²=13^2-5^2=144, erre m=12 adódik.
1
- Még nem érkezett komment!