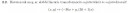Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Határozzuk meg az alábbi lineáris transzformáció sajátértékeit és sajátvektorait!
 kistar794
kérdése
kistar794
kérdése
380
(x, y) → (−6x + y,( 6 + 1)x)
ezt kellene valahogy megoldani, de öszintén szólva hozzá sem tudok kezdeni.
ezt kellene valahogy megoldani, de öszintén szólva hozzá sem tudok kezdeni.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A kép második koordinátáját biztos nem írtad el? Tényleg `(6+1)x`?
Ha helyes a kiírás, akkor az alábbi transzformációról van szó:
`[[x],[y]] mapsto [[-6x+y],[7x]]`
A transzformáció sajátvektorai azok a vektorok, amiket a transzformáció nem forgat el, hanem csak összenyom/megnyújt, vagyis skalárral szoroz. A szorzótényező pedig az ehhez a sajátvektorhoz tartozó sajátérték. Tehát a `\mathbf{T}` transzformáció sajátvektora `\mathbf{v}` és ehhez tartozó sajátértéke `lambda`, ha `\mathbf{T}\mathbf{v}=lambda \mathbf{v}`.
Először határozzuk meg a megadott transzformáció mátrixát! Ez úgy történik, hogy megnézzük, hová viszi a transzformáció a bázisvektorokat, majd az eredményvektorokat beírjuk egy mátrixba. Dolgozzunk a természetes bázisban, ekkor:
`[[1],[0]] mapsto [[-6],[7]]`
`[[0],[1]] mapsto [[1],[0]]`
Tehát a transzformáció természetes bázisbeli mátrixa:
`mathbf{T}=[[-6,1],[7,0]]`
Megvan a `\mathbf{T}` mátrix, most meg kell keresni a sajátértékeit és a sajátvektorait. Vagyis meg kell oldani a következő egyenletet:
`\mathbf{T}\mathbf{v}=lambda \mathbf{v}`
Nullára rendezve:
`(\mathbf{T}-lambda \mathbf{I})\mathbf{v}=\mathbf{0}`
Kiírva mátrixosan:
`[[-6-lambda,1],[7,-lambda]][[v_x],[v_y]]=[[0],[0]]`
Ahhoz, hogy a triviális `\mathbf{v}=\mathbf{0}`-tól különböző megoldása is legyen az egyenletnek, ahhoz az kell, hogy a mátrix determinánsa nulla legyen. Ebből jönnek ki a sajátértékek:
`|[-6-lambda,1],[7,-lambda]|``=``lambda (lambda+6)-7``=``lambda^2+6lambda-7=0`
Ez egy sima másodfokú egyenlet, a megoldóképlet alapján az jön ki, hogy a sajátértékek az alábbiak:
`lambda_1=1`
`lambda_2=-7`
Az `1` sajátértékhez tartozó sajátvektor:
`(\mathbf{T}-1*\mathbf{I})\mathbf{v}=\mathbf{0}`
`[[-7,1],[7,-1]][[v_x],[v_y]]=[[0],[0]]`
Innen például `\mathbf{v}_1=[[1],[7]]` jó lesz sajátvektornak. (A sajátvektorok nem egyértelműek, hiszen ha egy vektor sajátvektor, akkor tetszőleges skalárszorosa is az.)
A `-7` sajátértékhez tartozó sajátvektor:
`(\mathbf{T}+7*\mathbf{I})\mathbf{v}=\mathbf{0}`
`[[1,1],[7,7]][[v_x],[v_y]]=[[0],[0]]`
Ebből pedig például `\mathbf{v}_2=[[1],[-1]]`.
Ellenőrizzük le, hogy tényleg sajátvektorokat kaptunk-e. Nézzük meg, mit csinál a transzformáció a `\mathbf{v}_1` vektorral:
`[[1],[7]] mapsto [[-6*1+7],[7*1]]=[[1],[7]]`
Tehát a `\mathbf{v}_1` vektort a transzformáció helyben hagyja, vagyis `1`-gyel szorozza, ami éppen a `\mathbf{v}_1` sajátvektorhoz tartozó `lambda_1` sajátérték volt.
Hasonlóan nézzük meg, mit csinál a transzformáció a `\mathbf{v}_2` vektorral:
`[[1],[-1]] mapsto [[-6*1-1],[7*1]]=[[-7],[7]]`
Tehát a `\mathbf{v}_2` vektort a transzformáció `-7`-tel szorozza, ami éppen a `\mathbf{v}_2` sajátvektorhoz tartozó `lambda_2` sajátérték volt.
Ha helyes a kiírás, akkor az alábbi transzformációról van szó:
`[[x],[y]] mapsto [[-6x+y],[7x]]`
A transzformáció sajátvektorai azok a vektorok, amiket a transzformáció nem forgat el, hanem csak összenyom/megnyújt, vagyis skalárral szoroz. A szorzótényező pedig az ehhez a sajátvektorhoz tartozó sajátérték. Tehát a `\mathbf{T}` transzformáció sajátvektora `\mathbf{v}` és ehhez tartozó sajátértéke `lambda`, ha `\mathbf{T}\mathbf{v}=lambda \mathbf{v}`.
Először határozzuk meg a megadott transzformáció mátrixát! Ez úgy történik, hogy megnézzük, hová viszi a transzformáció a bázisvektorokat, majd az eredményvektorokat beírjuk egy mátrixba. Dolgozzunk a természetes bázisban, ekkor:
`[[1],[0]] mapsto [[-6],[7]]`
`[[0],[1]] mapsto [[1],[0]]`
Tehát a transzformáció természetes bázisbeli mátrixa:
`mathbf{T}=[[-6,1],[7,0]]`
Megvan a `\mathbf{T}` mátrix, most meg kell keresni a sajátértékeit és a sajátvektorait. Vagyis meg kell oldani a következő egyenletet:
`\mathbf{T}\mathbf{v}=lambda \mathbf{v}`
Nullára rendezve:
`(\mathbf{T}-lambda \mathbf{I})\mathbf{v}=\mathbf{0}`
Kiírva mátrixosan:
`[[-6-lambda,1],[7,-lambda]][[v_x],[v_y]]=[[0],[0]]`
Ahhoz, hogy a triviális `\mathbf{v}=\mathbf{0}`-tól különböző megoldása is legyen az egyenletnek, ahhoz az kell, hogy a mátrix determinánsa nulla legyen. Ebből jönnek ki a sajátértékek:
`|[-6-lambda,1],[7,-lambda]|``=``lambda (lambda+6)-7``=``lambda^2+6lambda-7=0`
Ez egy sima másodfokú egyenlet, a megoldóképlet alapján az jön ki, hogy a sajátértékek az alábbiak:
`lambda_1=1`
`lambda_2=-7`
Az `1` sajátértékhez tartozó sajátvektor:
`(\mathbf{T}-1*\mathbf{I})\mathbf{v}=\mathbf{0}`
`[[-7,1],[7,-1]][[v_x],[v_y]]=[[0],[0]]`
Innen például `\mathbf{v}_1=[[1],[7]]` jó lesz sajátvektornak. (A sajátvektorok nem egyértelműek, hiszen ha egy vektor sajátvektor, akkor tetszőleges skalárszorosa is az.)
A `-7` sajátértékhez tartozó sajátvektor:
`(\mathbf{T}+7*\mathbf{I})\mathbf{v}=\mathbf{0}`
`[[1,1],[7,7]][[v_x],[v_y]]=[[0],[0]]`
Ebből pedig például `\mathbf{v}_2=[[1],[-1]]`.
Ellenőrizzük le, hogy tényleg sajátvektorokat kaptunk-e. Nézzük meg, mit csinál a transzformáció a `\mathbf{v}_1` vektorral:
`[[1],[7]] mapsto [[-6*1+7],[7*1]]=[[1],[7]]`
Tehát a `\mathbf{v}_1` vektort a transzformáció helyben hagyja, vagyis `1`-gyel szorozza, ami éppen a `\mathbf{v}_1` sajátvektorhoz tartozó `lambda_1` sajátérték volt.
Hasonlóan nézzük meg, mit csinál a transzformáció a `\mathbf{v}_2` vektorral:
`[[1],[-1]] mapsto [[-6*1-1],[7*1]]=[[-7],[7]]`
Tehát a `\mathbf{v}_2` vektort a transzformáció `-7`-tel szorozza, ami éppen a `\mathbf{v}_2` sajátvektorhoz tartozó `lambda_2` sajátérték volt.
0
-
kistar794: válaszban csatoltam az eredeti képet 5 éve 0
 kistar794
válasza
kistar794
válasza
ez lett volna az eredeti kérdés, mindenkinek van egy "k" értéke ami nekem 2. Nem tudtam hogy ez befolyásolja
0
-
AlBundy: OK, ha neked `k=2`, akkor a fenti megoldás helyes. 5 éve 0
-
kistar794: nagyon köszönöm. 5 éve 0