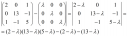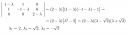Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

3x3-mas mátrix sajátértéke

386
Felírtam a | A-λE₃ | alakot és elkezdtem az egyenlet felírását (remélem jól).
Arra lennék kíváncsi, hogy valaki fel tudná-e írni az egyenletet olyan formában, amiből ki lehet olvasni, hogy mennyi a λ értéke (ÚGY mint a 2. képen)?
Az egyenletet levezettem teljesen, felbontva minden zárójelet, de a 3-mad fokú egyenletet nem tudnám megoldani magamtól.
Feladat kép
Feladat kép
Jelenleg 1 felhasználó nézi ezt a kérdést.
mátrix, Matematika, sajátérték, egyenlet
0
Felsőoktatás / Matematika

Válaszok

2
Itt egy 3. kép is arról, ahogy a felírást gondolom.
Válasz kép
0

A harmadik képen szereplő példa azért nagyon könnyű, mert ha a determinánst a 3. sor vagy oszlop szerint fejtjük ki, akkor csak egy tag lesz, így rögtön faktorizált formában kapjuk meg a karakterisztikus polinomot. A második képen meg ki lehetett emelni egy szép egész együtthatós teljes négyzetes tagot. A te példád sajnos nem ilyen szép, nem nagyon van mit tenni, mint megoldani a harmadfokú egyenletet. A karakterisztikus polinomot jól írtad fel:

`(2-lambda)(13-lambda)(5-lambda)-(2-lambda)-(13-lambda)``=``-lambda^3 + 20 lambda^2 - 99 lambda + 115`

A polinom még csak nem is hiányos, szimmetrikus, vagy egyéb módon speciális, a gyökei sem egészek, úgyhogy sok mindent nem lehet vele kezdeni. Ha mindenképp papíron kell megoldani, akkor a Wikipédián megtalálod a harmadfokú egyenlet megoldóképletét (nem olyan félelmetes). Ha elég a numerikus eredmény, akkor a tudományos számológépek szoktak tudni ilyet, illetve ott van a WolframAlpha is (https://bit.ly/3bacbDP). Ha már WolframAlpha, akkor egyébként közvetlenül a mátrixból is ki tudja számolni a sajátértékeket (https://bit.ly/2K9VWL1).
1