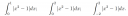Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Számítsa ki az alábbi integrálokat!
 Törölt
{ Kérdező } kérdése
Törölt
{ Kérdező } kérdése
323
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Esetszétválasztással tüntessük el az abszolútérték-jelet:
- ha `x le -1`, akkor `|x^2-1|=x^2-1`
- ha `-1 lt x lt 1`, akkor `|x^2-1|=1-x^2`
- ha `x ge 1`, akkor `|x^2-1|=x^2-1`
Ezek alapján fel tudjuk bontani résztartományokra az integrálokat. Az első:
`int_{0}^{1} |x^2-1| dx``=``int_{0}^{1} (1-x^2) dx``=``[x-x^3/3]_0^1``=``(1-1/3)-(0-0)``=``2/3`
A másodiknál fel tudjuk használni az első eredményét:
`int_{0}^{2} |x^2-1| dx``=``int_{0}^{1} (1-x^2) dx+int_{1}^{2} (x^2-1) dx``=``2/3+[x^3/3-x]_1^2``=``2/3+(8/3-2)-(1/3-1)``=``2`
A harmadiknál pedig kihasználhatjuk, hogy a függvény páros, tehát a grafikonja szimmetrikus az `y` tengelyre, így az integrál éppen az előző kétszerese lesz:
`int_{-2}^{2} |x^2-1| dx``=``2 int_{0}^{2} |x^2-1| dx=4`
Ha a paritást nem használjuk ki, akkor természetesen fapadosan is kiszámítható ugyanez:
`int_{-2}^{2} |x^2-1| dx``=``int_{-2}^{-1} (x^2-1) dx+int_{-1}^{1} (1-x^2) dx+int_{1}^{2} (x^2-1)dx=...`
Ajánlom figyelmedbe a WolframAlpha ábráját, sokat segíthet a megoldások megértésében: https://bit.ly/3erH9JK
- ha `x le -1`, akkor `|x^2-1|=x^2-1`
- ha `-1 lt x lt 1`, akkor `|x^2-1|=1-x^2`
- ha `x ge 1`, akkor `|x^2-1|=x^2-1`
Ezek alapján fel tudjuk bontani résztartományokra az integrálokat. Az első:
`int_{0}^{1} |x^2-1| dx``=``int_{0}^{1} (1-x^2) dx``=``[x-x^3/3]_0^1``=``(1-1/3)-(0-0)``=``2/3`
A másodiknál fel tudjuk használni az első eredményét:
`int_{0}^{2} |x^2-1| dx``=``int_{0}^{1} (1-x^2) dx+int_{1}^{2} (x^2-1) dx``=``2/3+[x^3/3-x]_1^2``=``2/3+(8/3-2)-(1/3-1)``=``2`
A harmadiknál pedig kihasználhatjuk, hogy a függvény páros, tehát a grafikonja szimmetrikus az `y` tengelyre, így az integrál éppen az előző kétszerese lesz:
`int_{-2}^{2} |x^2-1| dx``=``2 int_{0}^{2} |x^2-1| dx=4`
Ha a paritást nem használjuk ki, akkor természetesen fapadosan is kiszámítható ugyanez:
`int_{-2}^{2} |x^2-1| dx``=``int_{-2}^{-1} (x^2-1) dx+int_{-1}^{1} (1-x^2) dx+int_{1}^{2} (x^2-1)dx=...`
Ajánlom figyelmedbe a WolframAlpha ábráját, sokat segíthet a megoldások megértésében: https://bit.ly/3erH9JK
1
- Még nem érkezett komment!