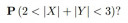Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Mi a valószínűsége a következő eseménynek?
 kapesmate
kérdése
kapesmate
kérdése
429
Ha X és Y N(0,1) független valószínűségi változók, akkor mi a valószínűsége a következő eseménynek (lásd a képen)?
Már próbáltam kiszámolni a képen látható változó együttes sűrűségfüggvényét. Valami kijött, de nem hinném, hogy jó, mert elég undorító az eredmény. Aztán megpróbáltam kiszámolni úgy, hogy az X és Y együttes sűrűségfüggvényt integráltam, méghozzá az (2,0);(3,0);(0,3);(0,2) tartományon, majd végül ezt szoroztam volna 4-gyel (mert 4 síknegyed van). A gond csak az, hogy az exp(-(x^2+y^2)/2) függvényt kell integrálnom véges tartományon. Valaki tud valami egyszerű megoldást, amihez nem kell wolfram alpha?
Már próbáltam kiszámolni a képen látható változó együttes sűrűségfüggvényét. Valami kijött, de nem hinném, hogy jó, mert elég undorító az eredmény. Aztán megpróbáltam kiszámolni úgy, hogy az X és Y együttes sűrűségfüggvényt integráltam, méghozzá az (2,0);(3,0);(0,3);(0,2) tartományon, majd végül ezt szoroztam volna 4-gyel (mert 4 síknegyed van). A gond csak az, hogy az exp(-(x^2+y^2)/2) függvényt kell integrálnom véges tartományon. Valaki tud valami egyszerű megoldást, amihez nem kell wolfram alpha?
Jelenleg 1 felhasználó nézi ezt a kérdést.
valszám, normális, gauss, integrál, eloszlás, sűrűségfüggvény
valszám, normális, gauss, integrál, eloszlás, sűrűségfüggvény
0
Felsőoktatás / Matematika
Válaszok
2 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Nem jött ki a végén egyszerű képlet, de azért elküldöm:
Kis egyszerűsítés először:
`P(2 < |x|+|y| < 3) = P(0 < |x|+|y| < 3)-P(0 < |x|+|y| < 2)`
és persze a 4 egyforma síknegyed miatt:
`= 4·(P(0 < x+y < 3)-P(0 < x+y ≤ 2))` ahol `x > 0` és `y > 0`
Így nem ferde csíkban kell integrálni, hanem háromszögben, az kicsit egyszerűbb.
(Természetesen a határokat (vagyis kisebb helyett kisebb-egyenlő) mindegy, hogy bevesszük vagy nem, annak az egyenesnek nulla a valószínűsége.)
Az egyik ilyen háromszögben (az `x+y=3` egyenes alatti területen) az integrál ez lesz:
`p_3=int_0^3 int_0^(3-x) 1/(2π) e^(-(x^2+y^2)/2) dy dx`
Menjünk át polárba:
`x=r·cos\ ω`
`y=r·sin\ ω`
A Jacobi determináns `r`, ezért `dxdy`-ból `r·drdω` lesz.
A szög megy 0-tól `π/2`-ig, a sugár pedig 0-tól a szögfüggő `r(ω)`-ig, ami így jön ki:
`x+y=r(ω)·(cos\ ω+sin\ ω)=3`
`r(ω)=3/(cos\ ω+sin\ ω)`
Az integrál tehát ez lesz:
`p_3=1/(2π) int_0^(π/2) int_0^(3/(cos\ ω+sin\ ω)) r·e^(-r^2/2)\ dr\ dω`
`p_3=1/(2π) int_0^(π/2) [-e^(-r^2/2)]_0^(3/(cos\ ω+sin\ ω))\ dω`
`p_3=1/(2π) int_0^(π/2) 1-e^(-3^2/(2(cos\ ω+sin\ ω)^2))\ dω`
és itt elakadtam...
Ha meglenne, akkor persze `4(p_3-p_2)` lenne a megoldás.
Matlabbal/Octave-val megoldható. Nem az kell? Mondjuk https://octave-online.net/
Eredeti integrál:
fun = @(x,y) exp( - (x.^2 + y.^2 )/2)/(2*pi); y2max = @(x) 2 - x; y3max = @(x) 3 - x;
4*(integral2(fun,0,3,0,y3max)-integral2(fun,0,2,0,y2max))
ans = 0.22321
A többit is kiszámoltam, csak hogy lássam, hogy nem rontottam el:
Poláros:
pol = @(omega,r) r.*exp(-(r.^2)/2)/(2*pi); rmax = @(m, omega) m ./ (sin(omega) + cos(omega));
r3max = @(omega) rmax(3, omega); r2max = @(omega) rmax(2, omega);
4*(integral2(pol,0,pi/2,0,r3max)-integral2(pol,0,pi/2,0,r2max))
ans = 0.22321
Vagy már a végső poláros képlet:
fun = @(m, omega) (1 .- exp(-(m.^2) ./ (2.*(sin(omega)+cos(omega)).^2)))./(2*pi);
fun2 = @(omega) fun(2, omega); fun3 = @(omega) fun(3, omega);
4*(integral(fun3,0,pi/2)-integral(fun2,0,pi/2))
ans = 0.22321
Kis egyszerűsítés először:
`P(2 < |x|+|y| < 3) = P(0 < |x|+|y| < 3)-P(0 < |x|+|y| < 2)`
és persze a 4 egyforma síknegyed miatt:
`= 4·(P(0 < x+y < 3)-P(0 < x+y ≤ 2))` ahol `x > 0` és `y > 0`
Így nem ferde csíkban kell integrálni, hanem háromszögben, az kicsit egyszerűbb.
(Természetesen a határokat (vagyis kisebb helyett kisebb-egyenlő) mindegy, hogy bevesszük vagy nem, annak az egyenesnek nulla a valószínűsége.)
Az egyik ilyen háromszögben (az `x+y=3` egyenes alatti területen) az integrál ez lesz:
`p_3=int_0^3 int_0^(3-x) 1/(2π) e^(-(x^2+y^2)/2) dy dx`
Menjünk át polárba:
`x=r·cos\ ω`
`y=r·sin\ ω`
A Jacobi determináns `r`, ezért `dxdy`-ból `r·drdω` lesz.
A szög megy 0-tól `π/2`-ig, a sugár pedig 0-tól a szögfüggő `r(ω)`-ig, ami így jön ki:
`x+y=r(ω)·(cos\ ω+sin\ ω)=3`
`r(ω)=3/(cos\ ω+sin\ ω)`
Az integrál tehát ez lesz:
`p_3=1/(2π) int_0^(π/2) int_0^(3/(cos\ ω+sin\ ω)) r·e^(-r^2/2)\ dr\ dω`
`p_3=1/(2π) int_0^(π/2) [-e^(-r^2/2)]_0^(3/(cos\ ω+sin\ ω))\ dω`
`p_3=1/(2π) int_0^(π/2) 1-e^(-3^2/(2(cos\ ω+sin\ ω)^2))\ dω`
és itt elakadtam...
Ha meglenne, akkor persze `4(p_3-p_2)` lenne a megoldás.
Matlabbal/Octave-val megoldható. Nem az kell? Mondjuk https://octave-online.net/
Eredeti integrál:
fun = @(x,y) exp( - (x.^2 + y.^2 )/2)/(2*pi); y2max = @(x) 2 - x; y3max = @(x) 3 - x;
4*(integral2(fun,0,3,0,y3max)-integral2(fun,0,2,0,y2max))
ans = 0.22321
A többit is kiszámoltam, csak hogy lássam, hogy nem rontottam el:
Poláros:
pol = @(omega,r) r.*exp(-(r.^2)/2)/(2*pi); rmax = @(m, omega) m ./ (sin(omega) + cos(omega));
r3max = @(omega) rmax(3, omega); r2max = @(omega) rmax(2, omega);
4*(integral2(pol,0,pi/2,0,r3max)-integral2(pol,0,pi/2,0,r2max))
ans = 0.22321
Vagy már a végső poláros képlet:
fun = @(m, omega) (1 .- exp(-(m.^2) ./ (2.*(sin(omega)+cos(omega)).^2)))./(2*pi);
fun2 = @(omega) fun(2, omega); fun3 = @(omega) fun(3, omega);
4*(integral(fun3,0,pi/2)-integral(fun2,0,pi/2))
ans = 0.22321
1
-
kapesmate: Na az, hogy áttérjek polárba, az eszembe sem jutott...de én is ugyanígy két háromszög különbségeként írtam fel, tehát a polár koordinátás felírásig megegyezik a megoldásunk... 5 éve 0
-
kapesmate: Találtam egy másik, sokkal egyszerűbb megoldást. Mivel az együttes sűrűségfüggvény forgásszimmetrikus, így az adott négyzet feletti valószínűség (amit háromszögek segítségével írtunk fel), az pontosan ugyanakkora mint ha a négyzetet elforgatjuk 45 fokkal. Így már csak sima eloszlásfüggvénybe kell behelyettesíteni, és kihasználni azt, hogy a két v.v. független, ezért szorzat alakba írható. 5 éve 0
 bongolo
{
bongolo
{  }
válasza
}
válasza
A forgatásos ötlet szupernek tűnik.
Gondolom megvan a megoldás, csak magamnak végigcsinálom én is:
Szóval vegyük az `x',y'` koordináta rendszert, ami 45 fokkal el van forgatva az `x,y`-hoz képest. A visszatranszformalás `(x';y')`-ből `(x;y)`-ba így megy:
`x=x'·cos\ 45°+y'·sin\ 45°`
`y=x'·sin\ 45°-y'·cos\ 45°`
Az `(x';y')` koordinátarendszerben az origó középpontú, a tengelyekkel párhuzamos oldalú négyzeten belüli területet kell integrálni. A négyzet `x'` és `y'`-ben is `-3·sqrt2/2` és `+3·sqrt2/2` közötti értékeket fed le. Tehát pl. az `(x';y')=(3·sqrt2/2; 3·sqrt2/2)` csúcspont visszaforgatva `x;y`-ba:
`x=x'·sqrt2/2+y'·sqrt2/2=3`
`y=x'·sqrt2/2-y'·sqrt2/2=0`
Vagyis a `(3;0)` pontba kerül.
A sűrűségfüggény tehát az eredeti `(x;y)` koordinátarendszerben:
`1/(2pi)e^(-(x^2+y^2)/2)`
A vesszősben pedig:
`x^2=((x')^2+(y')^2+2x'y')/2`
`y^2=((x')^2+(y')^2-2x'y')/2`
`x^2+y^2=(x')^2+(y')^2`
Tehát a sűrűségfüggvény integrálja a teljes tartományban (nem egy negyedben) :
(az egyszerűség kedvéért `x` és `y`-t írok, de mindkettő a vesszőset jelenti)
`int_(-3 sqrt2/2)^(3 sqrt2/2) int_(-3 sqrt2/2)^(3 sqrt2/2) 1/(2pi)e^(-(x^2+y^2)/2) dydx`
Hmm, ezt se lehet direktben integrálni... megint csak polárba kell menni:
Mondjuk a jobb oldali negyed `ω=-π/4` és `+π/4` között megy, a sugár pedig `r(ω)=(3sqrt2/2)/(cos\ ω)` lesz.
`p_3=1/(2pi)int_(-pi/4)^(pi/4) int_0^(3/(sqrt2 cos\ ω)) r·e^(-r^2/2)\ dr\ dω`
`p_3=1/(2pi)int_(-pi/4)^(pi/4) [ -e^(-r^2/2)]_0^(3/(sqrt2 cos\ ω))\ dω`
`p_3=1/(2pi)int_(-pi/4)^(pi/4) 1 - e^(-3^2/(4 cos^2 ω))\ dω`
Hmm, ez se lett egyszerűbb... ezt is csak numerikusan lehet kiszámolni. Vagy van még valamilyen másik trükk is?
Ja, OK, leesett... nem kell kifejezni képlettel, hanem a normális eloszlás táblázatából tudod kiszedni az eredményeket, aztán összeszorozni. Szóval kár volt szenvednem a poláros integrálással
`int_(-3 sqrt2/2)^(3 sqrt2/2) 1/sqrt(2pi)e^(-(x^2)/2) dx int_(-3 sqrt2/2)^(3 sqrt2/2) 1/sqrt(2pi)e^(-(y^2)/2) dy = (2·Φ(3 sqrt2/2)-1)^2`
A 2 és 3 közé esés valószínűsége pedig:
`(2·Φ(3 sqrt2/2)-1)^2-(2·Φ(2 sqrt2/2)-1)^2=0.2232`
Gondolom megvan a megoldás, csak magamnak végigcsinálom én is:
Szóval vegyük az `x',y'` koordináta rendszert, ami 45 fokkal el van forgatva az `x,y`-hoz képest. A visszatranszformalás `(x';y')`-ből `(x;y)`-ba így megy:
`x=x'·cos\ 45°+y'·sin\ 45°`
`y=x'·sin\ 45°-y'·cos\ 45°`
Az `(x';y')` koordinátarendszerben az origó középpontú, a tengelyekkel párhuzamos oldalú négyzeten belüli területet kell integrálni. A négyzet `x'` és `y'`-ben is `-3·sqrt2/2` és `+3·sqrt2/2` közötti értékeket fed le. Tehát pl. az `(x';y')=(3·sqrt2/2; 3·sqrt2/2)` csúcspont visszaforgatva `x;y`-ba:
`x=x'·sqrt2/2+y'·sqrt2/2=3`
`y=x'·sqrt2/2-y'·sqrt2/2=0`
Vagyis a `(3;0)` pontba kerül.
A sűrűségfüggény tehát az eredeti `(x;y)` koordinátarendszerben:
`1/(2pi)e^(-(x^2+y^2)/2)`
A vesszősben pedig:
`x^2=((x')^2+(y')^2+2x'y')/2`
`y^2=((x')^2+(y')^2-2x'y')/2`
`x^2+y^2=(x')^2+(y')^2`
Tehát a sűrűségfüggvény integrálja a teljes tartományban (nem egy negyedben) :
(az egyszerűség kedvéért `x` és `y`-t írok, de mindkettő a vesszőset jelenti)
`int_(-3 sqrt2/2)^(3 sqrt2/2) int_(-3 sqrt2/2)^(3 sqrt2/2) 1/(2pi)e^(-(x^2+y^2)/2) dydx`
Hmm, ezt se lehet direktben integrálni... megint csak polárba kell menni:
Mondjuk a jobb oldali negyed `ω=-π/4` és `+π/4` között megy, a sugár pedig `r(ω)=(3sqrt2/2)/(cos\ ω)` lesz.
`p_3=1/(2pi)int_(-pi/4)^(pi/4) int_0^(3/(sqrt2 cos\ ω)) r·e^(-r^2/2)\ dr\ dω`
`p_3=1/(2pi)int_(-pi/4)^(pi/4) [ -e^(-r^2/2)]_0^(3/(sqrt2 cos\ ω))\ dω`
`p_3=1/(2pi)int_(-pi/4)^(pi/4) 1 - e^(-3^2/(4 cos^2 ω))\ dω`
Hmm, ez se lett egyszerűbb... ezt is csak numerikusan lehet kiszámolni. Vagy van még valamilyen másik trükk is?
Ja, OK, leesett... nem kell kifejezni képlettel, hanem a normális eloszlás táblázatából tudod kiszedni az eredményeket, aztán összeszorozni. Szóval kár volt szenvednem a poláros integrálással

`int_(-3 sqrt2/2)^(3 sqrt2/2) 1/sqrt(2pi)e^(-(x^2)/2) dx int_(-3 sqrt2/2)^(3 sqrt2/2) 1/sqrt(2pi)e^(-(y^2)/2) dy = (2·Φ(3 sqrt2/2)-1)^2`
A 2 és 3 közé esés valószínűsége pedig:
`(2·Φ(3 sqrt2/2)-1)^2-(2·Φ(2 sqrt2/2)-1)^2=0.2232`
Módosítva: 5 éve
0
-
kapesmate: Igen, erről van szó...mondjuk itt úgy látom, hogy saroktól sarokig integrálsz, én azt csináltam hogy origotol (gyök18)/2ig egyik tengelyen majd masik iranyban 0 tol szinten (gyök18)/2-ig ... szoval egy kis negyzeten...ebbol a kis negyzetbol van minden siknegyeden igy megszoroztam 4gyel...de persze ugyanaz a két eredmény 5 éve 0