A hegy csúcsa és a tó szintmagassága közötti különbség `1250` `m`.
Tegyük fel, hogy a tó tükre semmilyen torzulást nem idéz elő, tehát ha
a turista közvetlenül a tó mellett állna, akkor a hegy tükörképének
látszólagos magassága szintén `1250` `m` lenne. Az `23° 20'` emelkedési
szögből kiszámolható a hegy `x` távolsága. Tehát `1250/x=tg(23° 20')`
alapján `x approx 2898` `m`. A `49° 30'` depressziós szögből pedig a hegy látszólagos `y` magasságát kapjuk vissza,
azaz `y/2898=tg(49,5°)` alapján `y approx 3393` `m`.
Ez pedig `1543` `m`-el több mint a hegy `1850` `m`-es tényleges magassága.
Tehát a turista `1543` `m`-es szintmagasságban tartózkodik.

(Folytatás az ábrával az ezt követő blokkban.)

A feladatban a turista helyzetéről a szögadatokon kivül semmit sem adtak meg. Két eset lehetséges. A természetjáró vagy a tó és a hegy között tartozkodik, vagy a tó egyik oldalán a hegy, míg a másik oldalán egy másik hegyoldalban maga a turista.

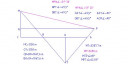
Nézzük az első esetet. Az előző blokk is ezt az esetet próbálta megoldani, de helytelen következtetésekre jutott. Az az elképzelés, hogy az emlelkedési szögből kiszámolható a hegy távolsága nem igaz, mert nem tudjuk, hogy a tárgyalandó szintkülönbözet (1250 m) hányadrésze esik ebbe a szögtartományba. A mellékelt ábrán látható, hogy a turista bárhol tartozkódhat az `MCO angle` szögtartományban, ahol `M` a hegycsúcsnak, `P` a turista helyzetének, `T` a hegycsúcs tükörképének, `OB` szakasz a tó vízszintjének felel meg. Így az első esetben nem kapunk egyértelmű megoldást. Az ábra azt az esetet mutatja, amikor a természetjáró `1200` `m`-es szinten tartozkodik. Ekkor is kijelölhető egy olyan `P` pont, ami a feladat feltételeit kielégíti.

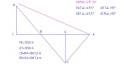
A másik esetben a turista egyértelmüen a tó egyik oldalán, míg a szóban forgó hegy a tó másik oldalán van. Ebben az esetben sem kapunk megoldást, mert a `23°20'` emelkedési szög nagynak tűnik ahhoz, hogy teljesítse a feladat feltételeit. Kiszámítható, hogy ez a küszöbérték `21,5°` (lásd az első ábrát; ahol `M` a hegycsúcsnak, `A` a turista helyének a tó szélénél, míg a `BC` szakasz a tó vízszintjének felel meg.) A `21,5°`-os küszöbértéknél kisebb `13° 20'`-es emelkedési szöget véve egyértelmű megoldáshoz jutunk. (lásd a második ábrát, ahol `P` a turista helyének és `T` a hegycsúcs tükörképének felel meg. ) Az 49,5° depressziós szög alapján kiszámítható a `CB` távoság. Ugyanis `tg(40,5°)=frac{CB}{1250}`, amiből `CB approx 1067,6` `m`. Amiből `CO=2135,2` `m` és a Pitagorasz-tétel alkalmazásával `MT=sqrt(2135,2^2+2500^2)=3287,7` `m`. Ezután az `MTP triangle`-ből a szinusz-tétellel kiszámítható az `MP` szakasz hossza.
`MP=frac{3287,7* sin(81°)}{sin(62,83°)}=3650` `m`.
Befejezésül szintén az `MTP triangle`-ből és a szinusz-tétel alkalmazásával nyerjük `frac{PT}{3650}=frac{sin(36,17°)}{sin(81°)}`, ahonnan
`PT=2181` `m`. `TA=frac{MT}{2} approx 1643,85` `m`. Hasonlósággal `frac{NC}{PA}=frac{OT}{TA}` és `PA=PT-TA` alkalmazásával nyerjük, hogy `NC=frac{537,17*1250}{1643,85}`, azaz `NC approx 408,5` `m`. Tehát a természetjáró `1008,5` `m`-es szinten tartozkodik.