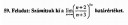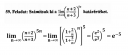Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika,határérték kiszámítása?
 Obit055
kérdése
Obit055
kérdése
794
Helló,valaki tudna segíteni ebben a feladatban?Utána néztem különböző limit calculator oldalakon,viszont egyiken sem kapok érthető levezetést,csak a végeredményt adják meg.
Előre is köszönöm
U.I: A képen n tart a végtelenbe,ha esetleg nem lehet tisztán kinézni.
Előre is köszönöm
U.I: A képen n tart a végtelenbe,ha esetleg nem lehet tisztán kinézni.
Jelenleg 1 felhasználó nézi ezt a kérdést.
Matematika, határérték, függvény
Matematika, határérték, függvény
0
Középiskola / Matematika
Válaszok
3 Törölt
{ Matematikus }
válasza
Törölt
{ Matematikus }
válasza
https://www.youtube.com/watch?v=IRKmPUh8_7E&list=PLwXxAxAEOlGgLDpzx1zVeSEOEFx257bDn&index=13
Ebben a videómban ezt a típust is magyarázom! Érdemes megnézned, ha szeretnéd tudni.
Ebben a videómban ezt a típust is magyarázom! Érdemes megnézned, ha szeretnéd tudni.
1
- Még nem érkezett komment!
 Törölt
{ Matematikus }
megoldása
Törölt
{ Matematikus }
megoldása
Amúgy ez a megoldás, de a videóm húszon valahányadik percében el is magyarázom a kívül belül ismeretlen, visíts fel, hogy EULER!
1
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Teljesen jók a fenti videó meg a levezetés, nekem is tetszik, fogadd el azt a választ megoldásnak.
Ennek ellenére én kicsit máshogy szoktam csinálni, ami néha gyorsabb megoldást ad (mondjuk az olyan feladatoknál, mint ami a videóban szintén van:
`lim_(n→∞)((3n-5)/(3n+4))^(7n-5) `
Először egy kis "segédtétel":
Amit meg kell jegyezni hozzá: (itt az `a, b, c, d` konstansok)
`lim_(n→∞)(1+a/n)^n=lim_(n→∞)(1+a/(n+b))^n=e^a`
vagy kicsit még tovább általánosítva:
`lim_(n→∞)(1+a/(n+b))^(cn+d)=e^(a·c)`
vagyis a `b` valamint `d` konstansok nem számítanak, mintha ott se lennének.
Fontos viszont az, hogy a zárójelen belül az `1` valamint az `n` nem lehet szorozva!
Ezeket nagyon könnyű levezetni, pl. az első így megy:
`lim_(n→∞)(1+a/(n+b))^n=lim_(n→∞)(1+a/(n+b))^((n+b)-b)=(lim_(n→∞)(1+a/(n+b))^(n+b) )/ (lim_(n→∞)(1+a/(n+b))^b)=`
`=(lim_(n+b→∞)(1+a/(n+b))^(n+b) )/ 1=e^a`
A másodikhoz se kell több ötlet, az is ugyanígy megy.
------------------------------------------------------------
És akkor az adott feladat:
`lim_(n→∞)((n+2)/(n+3))^(5n)=lim_(n→∞)((n+3-1)/(n+3))^(5n)=lim_(n→∞)(1+(-1)/(n+3))^(5n)=e^(-5)`
------------------------------------------------------------
Az a bonyolultabb feladat pedig, ami a videó 29-32-edik perceiben van:
`lim_(n→∞)((3n-5)/(3n+4))^(7n-5)=lim_(n→∞)((3n+4-9)/(3n+4))^(7n-5)=lim_(n→∞)(1+(-9)/(3n+4))^(7n-5)=`
`=lim_(n→∞)(1+(-3)/(n+4/3))^(7n-5)=e^(-3·7)=e^(-21)`
Ennek ellenére én kicsit máshogy szoktam csinálni, ami néha gyorsabb megoldást ad (mondjuk az olyan feladatoknál, mint ami a videóban szintén van:
`lim_(n→∞)((3n-5)/(3n+4))^(7n-5) `
Először egy kis "segédtétel":
Amit meg kell jegyezni hozzá: (itt az `a, b, c, d` konstansok)
`lim_(n→∞)(1+a/n)^n=lim_(n→∞)(1+a/(n+b))^n=e^a`
vagy kicsit még tovább általánosítva:
`lim_(n→∞)(1+a/(n+b))^(cn+d)=e^(a·c)`
vagyis a `b` valamint `d` konstansok nem számítanak, mintha ott se lennének.
Fontos viszont az, hogy a zárójelen belül az `1` valamint az `n` nem lehet szorozva!
Ezeket nagyon könnyű levezetni, pl. az első így megy:
`lim_(n→∞)(1+a/(n+b))^n=lim_(n→∞)(1+a/(n+b))^((n+b)-b)=(lim_(n→∞)(1+a/(n+b))^(n+b) )/ (lim_(n→∞)(1+a/(n+b))^b)=`
`=(lim_(n+b→∞)(1+a/(n+b))^(n+b) )/ 1=e^a`
A másodikhoz se kell több ötlet, az is ugyanígy megy.
------------------------------------------------------------
És akkor az adott feladat:
`lim_(n→∞)((n+2)/(n+3))^(5n)=lim_(n→∞)((n+3-1)/(n+3))^(5n)=lim_(n→∞)(1+(-1)/(n+3))^(5n)=e^(-5)`
------------------------------------------------------------
Az a bonyolultabb feladat pedig, ami a videó 29-32-edik perceiben van:
`lim_(n→∞)((3n-5)/(3n+4))^(7n-5)=lim_(n→∞)((3n+4-9)/(3n+4))^(7n-5)=lim_(n→∞)(1+(-9)/(3n+4))^(7n-5)=`
`=lim_(n→∞)(1+(-3)/(n+4/3))^(7n-5)=e^(-3·7)=e^(-21)`
0
-
Törölt: Valóban gyorsabb eljárás. És tetszik is. Az első átalakító lépést én egészrész leválasztásnak szoktam modani, de eddig csak számelméleti feladatoknál használtam. Köszönöm a kiegészítést, ma is tanultam valamit, amit érdemes megjegyeznem. 5 éve 0