Legyen az ismeretlen csúcs `v`!

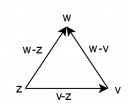
Ez lényegében egy koordinátageometriai feladat, csak itt a kétdimenziós koordináták egy-egy komplex számba vannak sűrítve. Ahogy a hagyományos koordinátageometriában megfeleltethetünk vektorokat a háromszög oldalainak (végpont koordinátái mínusz a kezdőpont koordinátái), úgy itt is megfeleltethetünk egy-egy komplex számot az egyes oldalaknak. Vegyük fel ezeket a mellékelt ábra szerint!

A szabályos háromszög oldalai ugyanolyan hosszúak, belső szögei 60 fokosak. Ez azt jelenti, hogy ha a `v-z` oldalt elforgatjuk pozitív irányba 60°-kal, akkor megkapjuk a `w-z` oldalt. Hasonlóan, ha a `w-v` oldalt forgatjuk el +60°-kal, akkor megkapjuk a `z-v` oldalt. Ha hagyományos koordinátageometriában lennénk, akkor a forgatás egy szinuszokkal és koszinuszokkal teli mátrixszal való szorzást jelentene. Szerencsére a komplex számok körében ez sokkal egyszerűbben leírható:

`w-z=e^(i pi/3) (v-z)`
`z-v=e^(i pi/3) (w-v)`

Elosztva egymással a két egyenletet:

`(w-z)/(z-v)=(v-z)/(w-v)`

Már csak ki kell fejezni ebből `v`-t:

`(w-z)(v-w)=(v-z)^2`

`wv+zv+zw=v^2+z^2+w^2`

`v^2+(-z-w)v+(z^2+w^2-zw)=0`

Ez `v`-re nézve egy másodfokú egyenlet, alkalmazható a megoldóképlet:

`v_{1,2}=(z+w pm sqrt((z+w)^2-4(z^2+w^2-zw)))/2``=``(z+w pm sqrt(-3z^2-3w^2+6zw))/2``=``(z+w pm sqrt(-3(z-w)^2))/2``=``(z+w pm i*sqrt(3)*(z-w))/2`

A súlypont pedig a megszokott módon számítható:

`s=(z+w+v)/3`