Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek
Tinaa
kérdése
515
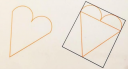
Egy 90,63 négyzetméter
területű „szívet” egy szabályos háromszögből és valamelyik oldalára illeszkedő két azonos sugarú félkörből raktak össze.
Határozza meg a szív kerületét!
területű „szívet” egy szabályos háromszögből és valamelyik oldalára illeszkedő két azonos sugarú félkörből raktak össze.
Határozza meg a szív kerületét!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1
magistratus
{ Tanár }
válasza
A szív területe megegyezik az őt felépítő szabályos háromszög és a kör (két félkör) területével. Legyen a háromszög oldalhossza `a`, ekkor a félkörök átmérője `frac(a)(2)`, sugaruk így `frac(a)(4)`.
`T_(text(szív))=T_(triangle)+T_(circ)=frac(a*a*sin 60°)(2)+(frac(a)(4))^2 *pi=frac(a^2*frac(sqrt(3))(2))(2)+frac(a^2)(16)*pi=`
`=frac(frac(a^2*sqrt(3))(2))(2)+frac(a^2*pi)(16)=frac(a^2*sqrt(3))(4)+frac(a^2*pi)(16)=frac(4a^2*sqrt(3))(16)+frac(a^2*pi)(16)=frac(4sqrt(3)a^2+pi a^2)(16)=`
`=frac(a^2(4sqrt(3)+pi))(16)`
`90text(,)63=frac(a^2(4sqrt(3)+pi))(16)`
`1450text(,)08=a^2(4sqrt(3)+pi)`
`144=a^2`
`a=pm12`
Mivel `a` háromszög oldala, ezért `a > 0`, tehát `a=12` m.
Ekkor a kerület:
`K_(text(szív))=(K_triangle-a)+K_circ=2a+2*(frac(a)(4))*pi=24+6piapprox42text(,)85` m
`T_(text(szív))=T_(triangle)+T_(circ)=frac(a*a*sin 60°)(2)+(frac(a)(4))^2 *pi=frac(a^2*frac(sqrt(3))(2))(2)+frac(a^2)(16)*pi=`
`=frac(frac(a^2*sqrt(3))(2))(2)+frac(a^2*pi)(16)=frac(a^2*sqrt(3))(4)+frac(a^2*pi)(16)=frac(4a^2*sqrt(3))(16)+frac(a^2*pi)(16)=frac(4sqrt(3)a^2+pi a^2)(16)=`
`=frac(a^2(4sqrt(3)+pi))(16)`
`90text(,)63=frac(a^2(4sqrt(3)+pi))(16)`
`1450text(,)08=a^2(4sqrt(3)+pi)`
`144=a^2`
`a=pm12`
Mivel `a` háromszög oldala, ezért `a > 0`, tehát `a=12` m.
Ekkor a kerület:
`K_(text(szív))=(K_triangle-a)+K_circ=2a+2*(frac(a)(4))*pi=24+6piapprox42text(,)85` m
0
- Még nem érkezett komment!