Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sokszög területének aránya
 atiny
kérdése
atiny
kérdése
1324
Egy szabályos sokszög szomszédos oldalfelező pontjait összekötjük, így egy újabb sokszöget kapunk. Számítsuk ki a beírt sokszög és a kiindulásul vett sokszög területének arányát, ha az oldalak száma 3!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 magistratus
{ Tanár }
válasza
magistratus
{ Tanár }
válasza
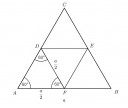
Szabályos `a` oldalhosszúságú háromszög oldalfelező pontjait összekötve nyilván háromszöget kapunk, de több is igaz, szabályos háromszöget fogunk kapni.
A `CABangle` nyilván `60^circ`-os, hiszen az `ABC_(triangle)` szabályos.
Viszont az `ADF_{triangle}` egyenlőszárú, `AD` és `AF` oldalai egyaránt `frac(a)(2)` hosszúak, így az alapon fekvő két szög `frac(180^circ-CABangle)(2)=frac(180^circ-60^circ)(2)=frac(120^circ)(2)=60^circ`-os.
`ADF_{triangle}` tehát nem csak egyenlőszárú, hanem mivel minden szöge `60^circ`-os, szabályos. Ezért a `DF` szintén `frac(a)(2)` hosszú.
Hasonlóan belátható, hogy `BFE_{triangle}` és `CDE_{triangle}` is szabályos, azaz `EF` és `DE` szakaszok is `frac(a)(2)` hosszúak.
`DEF_{triangle}` tehát egy `frac(a)(2)` oldalhosszúságú szabályos háromszög, azaz hasonló a nagy szabályos háromszöghöz, hasonlóságuk aránya pedig `lambda=frac(1)(2)`
Mivel két hasonló síkidomnál, ha a szakaszhosszak hasonlóságának aránya `lambda`, akkor a területeik aránya `lambda^2`, ezért a keresett területarány `lambda^2=frac(1)(4)`
(Megjegyzés: A hasonlóságos módszer helyett használható az is, hogy a nagy háromszöget 4 egybevágó részre bontottuk, így a kicsi területe épp negyede a nagy területének.)
A `CABangle` nyilván `60^circ`-os, hiszen az `ABC_(triangle)` szabályos.
Viszont az `ADF_{triangle}` egyenlőszárú, `AD` és `AF` oldalai egyaránt `frac(a)(2)` hosszúak, így az alapon fekvő két szög `frac(180^circ-CABangle)(2)=frac(180^circ-60^circ)(2)=frac(120^circ)(2)=60^circ`-os.
`ADF_{triangle}` tehát nem csak egyenlőszárú, hanem mivel minden szöge `60^circ`-os, szabályos. Ezért a `DF` szintén `frac(a)(2)` hosszú.
Hasonlóan belátható, hogy `BFE_{triangle}` és `CDE_{triangle}` is szabályos, azaz `EF` és `DE` szakaszok is `frac(a)(2)` hosszúak.
`DEF_{triangle}` tehát egy `frac(a)(2)` oldalhosszúságú szabályos háromszög, azaz hasonló a nagy szabályos háromszöghöz, hasonlóságuk aránya pedig `lambda=frac(1)(2)`
Mivel két hasonló síkidomnál, ha a szakaszhosszak hasonlóságának aránya `lambda`, akkor a területeik aránya `lambda^2`, ezért a keresett területarány `lambda^2=frac(1)(4)`
(Megjegyzés: A hasonlóságos módszer helyett használható az is, hogy a nagy háromszöget 4 egybevágó részre bontottuk, így a kicsi területe épp negyede a nagy területének.)
0
- Még nem érkezett komment!