Ezt nem levezetni kell, hanem mint egyenletet tekintve megoldani.

Kétféleképpen is lehetséges. Az egyik grafikus módszerrel ábrázolni a szóba jöhető függvényeket és a metszéspontokat megkeresni. A másik algebrai módszerekkel oldja meg az egyenletet.

Először nézzük az algebrai módszert.
Tudjuk, hogy `abs(x)={(x,bb "ha",x,ge,0),(-x,bb "ha",x,lt,0):}`. Ez azt jelenti, hogy
kétféle utat kell bejárni. Ha `x ge 0`, akkor `4x-2=x`, amire `x=frac{2}{3}`. Ha
`x lt 0`, akkor `4x-2=-x`, azaz `x=frac{2}{5}`, ami nemnegatív és ellentmondás.
Tehát az egyenlet egyetlen ellentmondást nem tűrő megoldása az `x=frac{2}{3}`.
Ellenőrzést rád bízom.

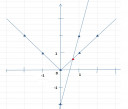
Nézzük a grafikus utat. Az a sejtésünk, hogy a megoldást az origó környezetében
érdemes keresni. Legyen `f(x):=4x-2` illetve `g(x):=abs(x)`.Vegyünk fel egy értéktáblázatot az `x=-2, -1,0,frac{2}{3},1,2` helyeken.
`[[x,-2, -1,0,frac{2}{3},1,2],[f(x),-10,-6,-2,frac{2}{3},2,6],[g(x),2, 1,0,frac{2}{3},1,2]]`Ebből kiolvasható, hogy a két függvény grafikonja a `P(frac{2}{3}; frac{2}{3})` helyen metszi egymást. (Lásd a csatolt képet)