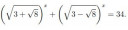Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Egyenletek
mateKos
kérdése
2465
Oldd meg a valós számok halmazán a következő egyenletet
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, Matematika, egyenlet, egyenlőtlenség, négyzet, Gyökvonás, egyentelek
matek, Matematika, egyenlet, egyenlőtlenség, négyzet, Gyökvonás, egyentelek
0
Középiskola / Matematika
Válaszok
2
gyula205
válasza
WolframAlpha segítségével az egyenletnek két gyöke is van: `x_1=-4` ill. `x_2=4`.
Ez gondolom nem elég, szükségünk van a levezetésre is.
Szorozzuk meg az egyenletet az egyik ismeretlent tartalmazó taggal.
Legyen ez `y=sqrt(3-sqrt(8))` és egyúttal új ismeretlen is. Kapunk egy másodfokú
egyenletet: ` y^2-34y+1=0` és a megoldása `y_(1,2)=17 pm 12*sqrt(2)`. Viszont
a `(3-sqrt(8))^2=17-12*sqrt(2)` ill. `(3-sqrt(8))^(-2)=17+12*sqrt(2)`. Ebből
már következik a már leírt állítás is.
Ez gondolom nem elég, szükségünk van a levezetésre is.
Szorozzuk meg az egyenletet az egyik ismeretlent tartalmazó taggal.
Legyen ez `y=sqrt(3-sqrt(8))` és egyúttal új ismeretlen is. Kapunk egy másodfokú
egyenletet: ` y^2-34y+1=0` és a megoldása `y_(1,2)=17 pm 12*sqrt(2)`. Viszont
a `(3-sqrt(8))^2=17-12*sqrt(2)` ill. `(3-sqrt(8))^(-2)=17+12*sqrt(2)`. Ebből
már következik a már leírt állítás is.
Módosítva: 6 éve
-1
-
bongolo: Mármint `y=sqrt(3-sqrt8)^x`, ugye?? A végén pedig, ha nem nézed meg a Wolfram-on, nem nagyon lehet rájőnni, hogy miért lesz x=2... 6 éve 0
-
bongolo: A másodfokú megoldása nem `x_"1,2"`, hanem `y_"1,2"` 6 éve 0
-
bongolo: És nem `17+-sqrt2`, hanem `17+-12sqrt2` ... 6 éve 0
-
bongolo: Ráadásul nem `+-2`, hanem `+-4` a megoldás... 6 éve 0
-
bongolo: `(sqrt(3+sqrt8))^2+(sqrt(3-sqrt8))^2=3+3=6`, nem pedig 34. 6 éve 0
-
bongolo: Szóval nem jó a 2. 6 éve 0
-
gyula205: Igen a külső gyököt lefelejtve oldottam meg, de már csinálom is a javítást. Köszönöm. 6 éve 0
bongolo
{ 
}
megoldása
Ezeket a gyökös gyököket át lehet alakítani egyszerűbbre:
`sqrt(3+sqrt8)=sqrt(3+2sqrt2)=a+b sqrt2`
`3+2sqrt2=a^2+2ab sqrt2+2b^2`
Vagyis:
`a^2+2b^2=3`
`2ab sqrt2=2 sqrt2 \ \ ` → `\ \ ab=1`
Ami `a=b=1` esetén teljesül.
Vagyis `sqrt(3+sqrt8)=1+sqrt2`
Hasonlóképpen kijön, hogy `sqrt(3-sqrt8)=sqrt2-1`
Az még gyorsabban látszik, hogy `(sqrt2+1)(sqrt2-1)=1`, vagyis ezek egymás reciprokai. A feladat tehát:
`(1+sqrt2)^x+(1+sqrt2)^(-x)=34`
Ez pedig azt jelenti, hogy ha van egy `x` megoldás, akkor a `"-"x` is megoldás.
Legyen `y=(1+sqrt2)^x`
`y+1/y=34`
`y^2-34y+1=0`
`y_"1,2"=17 +- 12sqrt2`
Könnyen látszik, hogy ez a két megoldás is egymás reciprokai (szorozd össze őket; `17^2=289`, `2·12^2=288`), ami azt jelenti, hogy az egyik a pozitív `x`-hez, a másik a negatív `"-"x`-hez tartozik. Elég csak a pozitívat nézni:
`(1+sqrt2)^x=17 + 12sqrt2`
`x=(log(17 + 12sqrt2))/(log(1+sqrt2))`
Ez az egyik megoldás, a másik pedig a negáltja.
Ezzel már akár meg is vagyunk, de ha feltételezzük, hogy hátha ez egy egész szám, jó lenne a pontos értéket megadni. Egyrészt persze csinálhatjuk azt, hogy számológéppel kiszámoljuk a logaritmus meg a tört értékét amilyen pontossággal a számológép tudja, aztán megnézzük, hogy az egészre kerekített érték valódi megoldás-e. Vagy gondolkodhatunk így:
`(1+sqrt2)^n=1+n·sqrt2+((n),(2))·2+((n),(3))·2sqrt2+((n),(4))·2^2+...`
Ennek kell `17 + 12sqrt2`-nek lennie. Vagyis:
`1+((n),(2))·2+((n),(4))·2^2+...=17`
`(n+((n),(3))·2+...)sqrt2=12 sqrt2`
Ami bal oldalak nagyon gyorsan elkezdenek elszaladni `n` növelésével, gyorsan kiderül, hogy `n=4` vagyis `x=4` a megoldás. Meg persze a `-4` is...
`sqrt(3+sqrt8)=sqrt(3+2sqrt2)=a+b sqrt2`
`3+2sqrt2=a^2+2ab sqrt2+2b^2`
Vagyis:
`a^2+2b^2=3`
`2ab sqrt2=2 sqrt2 \ \ ` → `\ \ ab=1`
Ami `a=b=1` esetén teljesül.
Vagyis `sqrt(3+sqrt8)=1+sqrt2`
Hasonlóképpen kijön, hogy `sqrt(3-sqrt8)=sqrt2-1`
Az még gyorsabban látszik, hogy `(sqrt2+1)(sqrt2-1)=1`, vagyis ezek egymás reciprokai. A feladat tehát:
`(1+sqrt2)^x+(1+sqrt2)^(-x)=34`
Ez pedig azt jelenti, hogy ha van egy `x` megoldás, akkor a `"-"x` is megoldás.
Legyen `y=(1+sqrt2)^x`
`y+1/y=34`
`y^2-34y+1=0`
`y_"1,2"=17 +- 12sqrt2`
Könnyen látszik, hogy ez a két megoldás is egymás reciprokai (szorozd össze őket; `17^2=289`, `2·12^2=288`), ami azt jelenti, hogy az egyik a pozitív `x`-hez, a másik a negatív `"-"x`-hez tartozik. Elég csak a pozitívat nézni:
`(1+sqrt2)^x=17 + 12sqrt2`
`x=(log(17 + 12sqrt2))/(log(1+sqrt2))`
Ez az egyik megoldás, a másik pedig a negáltja.
Ezzel már akár meg is vagyunk, de ha feltételezzük, hogy hátha ez egy egész szám, jó lenne a pontos értéket megadni. Egyrészt persze csinálhatjuk azt, hogy számológéppel kiszámoljuk a logaritmus meg a tört értékét amilyen pontossággal a számológép tudja, aztán megnézzük, hogy az egészre kerekített érték valódi megoldás-e. Vagy gondolkodhatunk így:
`(1+sqrt2)^n=1+n·sqrt2+((n),(2))·2+((n),(3))·2sqrt2+((n),(4))·2^2+...`
Ennek kell `17 + 12sqrt2`-nek lennie. Vagyis:
`1+((n),(2))·2+((n),(4))·2^2+...=17`
`(n+((n),(3))·2+...)sqrt2=12 sqrt2`
Ami bal oldalak nagyon gyorsan elkezdenek elszaladni `n` növelésével, gyorsan kiderül, hogy `n=4` vagyis `x=4` a megoldás. Meg persze a `-4` is...
0
-
gyula205: Most már minden rendben van. 6 éve 0