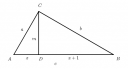
Jelölésekért lásd a csatolmányt.
`c=x+(x+1)=2x+1`, ennél a feladat szövege szerint a kisebbik befogó, `a`, 1-gyel kisebb: `a=c-1=(2x+1)-1=2x`.

I. MEGOLDÁS
Ha észre vesszük, hogy az `ACD` félszabályos háromszög

Észre vesszük, hogy az `ACD` derékszögű háromszög átfogója, `a=2x`, éppen kétszerese az egyik befogójának, ami `x`. Ez tehát egy speciális, félszabályos háromszög (szögei 30°, 60°, és 90°, valamint `m`-re, mint tengelyre tükrözve szabályos háromszöget kapnánk).
Mivel a derékszögű háromszöget az átfogóhoz tartozó magasság két olyan hasonló derékszögű háromszögre bontja, amik az eredeti nagy háromszöghöz is hasonlók (ugyanakkorák a megfelelő szögeik), ezért `ABC` és `ACD` háromszögek hasonlók, tehát az eredeti nagy háromszög is félszabályos háromszög.
Ebből viszont következik, hogy az átfogó a rövidebb befogó kétszerese, azaz:
`c=2a`
`2x+1=2 \cdot 2x`
`\frac{1}{2}` cm `=x`.

Innen a megoldás egyezik a II. megoldáséval a *-tól

II. MEGOLDÁS
Ha nem vesszük észre, hogy az `ACD` félszabályos háromszög

A derékszögű háromszöget az átfogóhoz tartozó magasság két olyan hasonló derékszögű háromszögre bontja, amik az eredeti nagy háromszöghöz is hasonlók (ugyanakkorák a megfelelő szögeik), ezért `ABC` és `ACD` háromszögek hasonlók.
A megfelelő oldalak aránya:
`\frac{a}{x}=\frac{c}{a}`
Behelyettesítve:
`\frac{2x}{x}=\frac{2x+1}{2x}`
Ezt megszorozva `2x`-szel:
`4x=2x+1`
`x=\frac{1}{2}` cm.

*
Ebből `a=2x=2\cdot\frac{1}{2}=1` cm, `c=2x+1=2\cdot\frac{1}{2}+1=2` cm.
`b` innen Pitagorasz tétellel könnyen számítható:
`b=\sqrt{c^2-a^2}=\sqrt{2^2-1^2}=\sqrt{4-1}=\sqrt{3}` cm.