Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Társas
 kapesmate
kérdése
kapesmate
kérdése
376
Mi a valószínűsége, hogy egy 1,2,3,... számozású mezőkből álló társasjátéknál az n. mezőre fogok valaha lépni (végtelen hosszú a társas), ha pontosan annyit lépek, mint amennyit dobok egy szabályos kockával?
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, valszám, markov, független, idő, invariancia, Valószínűség, véges, kombiantorika, Pascal
matek, valszám, markov, független, idő, invariancia, Valószínűség, véges, kombiantorika, Pascal
0
Felsőoktatás / Matematika
Válaszok
2 kapesmate
válasza
kapesmate
válasza
Természetesen megengedett a több lépés, tehát hogy többször dobjak.
0
- Még nem érkezett komment!
 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Jelentse `P_n` annak a valószínűségét, hogy valaha elérjük az `n`-edik mezőt. Feltételezem, hogy a táblán kívülről, a "nullás mezőről" indulunk (ha az 1-es számú mezőről indulunk, akkor pontosan ugyanígy kell csinálni, de sokkal rondább komplex számok jönnek ki). Akkor fogjuk elérni az `n`-edik mezőt, ha a kockadobásaink összege valamikor éppen `n` lesz.
`P_1=1/6`, mert az 1-es mezőt csak úgy érhetjük el, ha az első dobásunk 1.
`P_2=1/6+1/6 P_1 = 7/36`, mert a 2-es mezőt kétféleképpen érhetjük el: vagy az első dobásunk 2-es, vagy az 1-es mezőn állva 1-est dobunk.
`P_3=1/6 + 1/6 P_1 + 1/6 P_2=49/216`, mert úgy kerülhetünk a 3-as mezőre, hogy elsőre 3-ast dobunk, vagy az 1-es mezőn állva 2-est dobunk, vagy pedig a 2-es mezőn állva 1-est dobunk.
`P_4=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3=343/1296`
`P_5=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3 + 1/6 P_4=771/2497`
`P_6=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3 + 1/6 P_4 + 1/6 P_5=558/1549`
`n>6`-ra:
`P_n=1/6 P_{n-1}+1/6 P_{n-2}+1/6 P_{n-3}+1/6 P_{n-4}+1/6 P_{n-5}+1/6 P_{n-6}`
Ez egy lineáris rekurzió. A karakterisztikus egyenlete:
`q^6=1/6 q^5+1/6 q^4+1/6 q^3+1/6 q^2+1/6 q+1/6`
`6q^6-q^5-q^4-q^3-q^2-q-1=0`
A hatodfokú egyenletet megoldja nekünk pl. a WolframAlpha, a gyökök az alábbiak:
`q_1=1`
`q_2~~-0.670332`
`q_{3,4}~~-0.375695 pm 0.570175 i``~~``0.682823 e^(pm2.153411i)`
`q_{5,6}~~0.294195 pm 0.668367 i``~~``0.730250 e^(pm1.156148i)`
A rekurzió megoldásterének bázisát a fentiek hatványai adják. A megoldandó egyenletrendszer a következő:
`P_1=c_1 q_1 +c_2 q_2 +c_3 q_3 +c_4 q_4 +c_5 q_5 +c_6 q_6`
`P_2=c_1 q_1^2 +c_2 q_2^2 +c_3 q_3^2 +c_4 q_4^2 +c_5 q_5^2 +c_6 q_6^2`
...
`P_6=c_1 q_1^6 +c_2 q_2^6 +c_3 q_3^6 +c_4 q_4^6 +c_5 q_5^6 +c_6 q_6^6`
Ez is mehet WolframAlphával vagy tetszőleges más programmal (Python szkriptet mellékeltem képként). A megoldások:
`c_1=2/7`
`c_2=c_3=c_4=c_5=c_6=1/7`
Ezek után a keresett valószínűség:
`P_n = sum_{i=1}^6 c_i q_i^n=`
`2/7+1/7((-0.670332)^n``+``0.682823^n (e^(n*2.153411i)+e^(-n*2.153411i))``+``0.730250^n (e^(n*1.156148i)+e^(-n*1.156148i)))=`
`2/7+1/7*(-0.670332)^n``+``2/7*0.682823^n*cos(n*2.153411)``+``2/7*0.730250^n*cos(n*1.156148)`
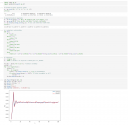
Mellékeltem egy Python nyelvű szimulációt, ami 1-től 100-ig minden `n`-re lejátszik húszezer játékot. Jól látszik, hogy a szimuláció eredménye szépen követi az elméleti számítást. Az is látszik, hogy nagy `n`-re a valószínűség `2/7`-hez tart. Ez a levezetett kifejezésből is könnyen látható, hiszen az egynél kisebb alapú exponenciális tagok a végtelenben nullához tartanak.
`P_1=1/6`, mert az 1-es mezőt csak úgy érhetjük el, ha az első dobásunk 1.
`P_2=1/6+1/6 P_1 = 7/36`, mert a 2-es mezőt kétféleképpen érhetjük el: vagy az első dobásunk 2-es, vagy az 1-es mezőn állva 1-est dobunk.
`P_3=1/6 + 1/6 P_1 + 1/6 P_2=49/216`, mert úgy kerülhetünk a 3-as mezőre, hogy elsőre 3-ast dobunk, vagy az 1-es mezőn állva 2-est dobunk, vagy pedig a 2-es mezőn állva 1-est dobunk.
`P_4=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3=343/1296`
`P_5=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3 + 1/6 P_4=771/2497`
`P_6=1/6+1/6 P_1 + 1/6 P_2 + 1/6 P_3 + 1/6 P_4 + 1/6 P_5=558/1549`
`n>6`-ra:
`P_n=1/6 P_{n-1}+1/6 P_{n-2}+1/6 P_{n-3}+1/6 P_{n-4}+1/6 P_{n-5}+1/6 P_{n-6}`
Ez egy lineáris rekurzió. A karakterisztikus egyenlete:
`q^6=1/6 q^5+1/6 q^4+1/6 q^3+1/6 q^2+1/6 q+1/6`
`6q^6-q^5-q^4-q^3-q^2-q-1=0`
A hatodfokú egyenletet megoldja nekünk pl. a WolframAlpha, a gyökök az alábbiak:
`q_1=1`
`q_2~~-0.670332`
`q_{3,4}~~-0.375695 pm 0.570175 i``~~``0.682823 e^(pm2.153411i)`
`q_{5,6}~~0.294195 pm 0.668367 i``~~``0.730250 e^(pm1.156148i)`
A rekurzió megoldásterének bázisát a fentiek hatványai adják. A megoldandó egyenletrendszer a következő:
`P_1=c_1 q_1 +c_2 q_2 +c_3 q_3 +c_4 q_4 +c_5 q_5 +c_6 q_6`
`P_2=c_1 q_1^2 +c_2 q_2^2 +c_3 q_3^2 +c_4 q_4^2 +c_5 q_5^2 +c_6 q_6^2`
...
`P_6=c_1 q_1^6 +c_2 q_2^6 +c_3 q_3^6 +c_4 q_4^6 +c_5 q_5^6 +c_6 q_6^6`
Ez is mehet WolframAlphával vagy tetszőleges más programmal (Python szkriptet mellékeltem képként). A megoldások:
`c_1=2/7`
`c_2=c_3=c_4=c_5=c_6=1/7`
Ezek után a keresett valószínűség:
`P_n = sum_{i=1}^6 c_i q_i^n=`
`2/7+1/7((-0.670332)^n``+``0.682823^n (e^(n*2.153411i)+e^(-n*2.153411i))``+``0.730250^n (e^(n*1.156148i)+e^(-n*1.156148i)))=`
`2/7+1/7*(-0.670332)^n``+``2/7*0.682823^n*cos(n*2.153411)``+``2/7*0.730250^n*cos(n*1.156148)`
Mellékeltem egy Python nyelvű szimulációt, ami 1-től 100-ig minden `n`-re lejátszik húszezer játékot. Jól látszik, hogy a szimuláció eredménye szépen követi az elméleti számítást. Az is látszik, hogy nagy `n`-re a valószínűség `2/7`-hez tart. Ez a levezetett kifejezésből is könnyen látható, hiszen az egynél kisebb alapú exponenciális tagok a végtelenben nullához tartanak.
1
-
kapesmate: Nagyon köszönöm! 6 éve 0