Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Felszín
 Fülöp Nikoletta
kérdése
Fülöp Nikoletta
kérdése
635
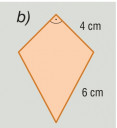
Mekkora a felszíne annak a 10 cm magasságú hasábnak, amelynek felülnézete az ábrán látható?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Általános iskola / Matematika
Válaszok
1 AnnaLola
megoldása
AnnaLola
megoldása
2Az egész hasáb területe az alábbiakból tevődik össze
2db deltoid
2db 4x10-es téglalap
2db 6x10-es téglalap
Ezeknek kiszámolod a területét és összeadod
A deltoid területét az e*f/2 képlettel tudod kiszámolni
az "e" átlót pitagorasz-tétellel tudjuk kiszámolni (megvan adva a két befogó, amik 4cm-esek és meg van adva ugye a derékszög)
Tehát
e2=42+42
e2=32
e=4√ 2
Az "f" átlót ugyanígy pitagorasz tétellel tudjuk kiszámolni, tudjuk, hogy az "f" átló felezi az "e" átlót, így kapunk egy olyan derékszögú háromszöget, aminek az átfogója 4cm, az egyik befogója 4√ 2 /2 (ugye az "e"-nek a fele), a másik befogója pedig f/3 (mivel az "e" átló 1/3 és 2/3 arányban metszi az "f" átlót)
Tehát
42=(4√ 2 /2)2+f/32
16=8+f/3
8=f/3
f=24
Így megvan a két átló, a deltoid területképletébe behelyettesítjük
T=ef/2
T=4√ 2 *24/2
T=48√ 2
És ahogy az elején írtam, kiszámolod még a téglalapok területét
T=6*10=60
T=4*10=40
Ezeket összeadod, ahogy az elején írtam
A=2*48√ 2 +2*60+2*40
A=335.764502cm2
Remélem követhető voltam
2db deltoid
2db 4x10-es téglalap
2db 6x10-es téglalap
Ezeknek kiszámolod a területét és összeadod
A deltoid területét az e*f/2 képlettel tudod kiszámolni
az "e" átlót pitagorasz-tétellel tudjuk kiszámolni (megvan adva a két befogó, amik 4cm-esek és meg van adva ugye a derékszög)
Tehát
e2=42+42
e2=32
e=4√ 2
Az "f" átlót ugyanígy pitagorasz tétellel tudjuk kiszámolni, tudjuk, hogy az "f" átló felezi az "e" átlót, így kapunk egy olyan derékszögú háromszöget, aminek az átfogója 4cm, az egyik befogója 4√ 2 /2 (ugye az "e"-nek a fele), a másik befogója pedig f/3 (mivel az "e" átló 1/3 és 2/3 arányban metszi az "f" átlót)
Tehát
42=(4√ 2 /2)2+f/32
16=8+f/3
8=f/3
f=24
Így megvan a két átló, a deltoid területképletébe behelyettesítjük
T=ef/2
T=4√ 2 *24/2
T=48√ 2
És ahogy az elején írtam, kiszámolod még a téglalapok területét
T=6*10=60
T=4*10=40
Ezeket összeadod, ahogy az elején írtam
A=2*48√ 2 +2*60+2*40
A=335.764502cm2
Remélem követhető voltam

0
-
DeeDee: "(mivel az "e" átló 1/3 és 2/3 arányban metszi az "f" átlót)" - Ez biztos igaz? 6 éve 0
-
DeeDee: Nem gyanús, hogy a hosszabbik átló hosszabb mint a deltoid két oldalának összege? 6 éve 0
-
AnnaLola: Akkor mi a te megoldásod?
 5 éve
0
5 éve
0