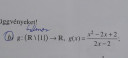Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Függvény egyenlet
 Aladarka
kérdése
Aladarka
kérdése
608
A kerdesem az lenne, hogy ezt az egyenletet (kep)hogy alakitom at abrazolhato formaba?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Az első taktika az ilyen típusú függvényeknél, hogy kiszámolod a számláló és a nevező gyökeit, aztán átírod gyöktényezős alakba, végül látod, hogy mivel lehet egyszerűsíteni, például, ha mindkettőnek gyöke az 5, akkor a gyöktényezős alakban lesz (x-5), és ezekkel tudsz egyszerűsíteni.
Ebben az esetben a számlálónak nincs is gyöke, úgyhogy ezzel nem tudunk mit kezdeni, így másik utat kell választanunk; először kiemelünk 2-t a nevezőből:
(1/2) * (x²-2x+2)/(x-1), ezután a számlálót teljes négyzetté alakítjuk:
(1/2) * ((x-1)²+1)/(x-1), és itt már tudunk osztani:
(1/2) * (x-1 +1/(x-1))
Ha most elfeledkezünk az 1/2-ről, akkor egy olyan függvényt kapunk, ahol egy szám és annak a reciprokának összege látható. A függvénytranszformációs szabályok szerint arra is hamar rá lehet jönni, hogy az x+(1/x) függvény eltoltja, ezt könnyen tudjuk ábrázolni, mivel az x=1 helyen minimuma van, ami 2, egyébként x≥1-re igaz az, hogy f(c)=f(1/c), tehát például az f(5) helyen ugyanazt a függvényértéket veszi fel, mint az f(1/5) helyen. Arra is hamar rá lehet jönni, hogy ez a függvény páratlan, vagyis f(x)=-f(-x) teljesül, tehát az x>0 ágát csak tükrözni kell az origóra. Ha ezzel megvagyunk, akkor az (1/2)-es szorzó miatt össze kell lapítani a függvény, aztán hogy (1/2)*(x+(1/x))-ből (1/2)*(x-1+(1/(x-1)) legyen, el kell tolni 1-gyel jobbra.
A WolframAlpha egyébként szépen kirajzolja a függvényt:
http://www.wolframalpha.com/input/?i=(x%5E2-2x%2B2)%2F(2x-2)
Ebben az esetben a számlálónak nincs is gyöke, úgyhogy ezzel nem tudunk mit kezdeni, így másik utat kell választanunk; először kiemelünk 2-t a nevezőből:
(1/2) * (x²-2x+2)/(x-1), ezután a számlálót teljes négyzetté alakítjuk:
(1/2) * ((x-1)²+1)/(x-1), és itt már tudunk osztani:
(1/2) * (x-1 +1/(x-1))
Ha most elfeledkezünk az 1/2-ről, akkor egy olyan függvényt kapunk, ahol egy szám és annak a reciprokának összege látható. A függvénytranszformációs szabályok szerint arra is hamar rá lehet jönni, hogy az x+(1/x) függvény eltoltja, ezt könnyen tudjuk ábrázolni, mivel az x=1 helyen minimuma van, ami 2, egyébként x≥1-re igaz az, hogy f(c)=f(1/c), tehát például az f(5) helyen ugyanazt a függvényértéket veszi fel, mint az f(1/5) helyen. Arra is hamar rá lehet jönni, hogy ez a függvény páratlan, vagyis f(x)=-f(-x) teljesül, tehát az x>0 ágát csak tükrözni kell az origóra. Ha ezzel megvagyunk, akkor az (1/2)-es szorzó miatt össze kell lapítani a függvény, aztán hogy (1/2)*(x+(1/x))-ből (1/2)*(x-1+(1/(x-1)) legyen, el kell tolni 1-gyel jobbra.
A WolframAlpha egyébként szépen kirajzolja a függvényt:
http://www.wolframalpha.com/input/?i=(x%5E2-2x%2B2)%2F(2x-2)
0
-
Aladarka: A harmadik bekezdesedben azt irtad hogy tudunk osztani es az x-1rol 9 éve 0
-
Aladarka: Leesett a negyzet de a nevezoben ott maradt az x-1 9 éve 0
-
Rantnad: Igen, és osztottunk is vele. 9 éve 0
-
Aladarka: De akkor a nevezoben miert maradt ott? 9 éve 0
 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Általános iskolában megtanultuk, hogy például (2/9)+(5/9)=(2+5)/9=7/9. Értelemszerűen ez egy megfordítható művelet, tehát a 7/9-ből tudunk (2/9)+(5/9)-et csinálni.
Ebben a feladatban is ugyanezt a történet: ((x-1)²+1)/(x-1)=(x-1)²/(x-1) + 1/(x-1), az első tört értéke x-1, tehát eredménynek (x-1) + 1/(x-1)-et kapunk.
Ebben a feladatban is ugyanezt a történet: ((x-1)²+1)/(x-1)=(x-1)²/(x-1) + 1/(x-1), az első tört értéke x-1, tehát eredménynek (x-1) + 1/(x-1)-et kapunk.
0
-
Aladarka: Es a 1/2hova tunt? 9 éve 0
-
Rantnad: "...először kiemelünk 2-t a nevezőből", oda. 9 éve 0