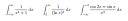Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Konvergensek-e az alábbi improprius integrálok?
 akosfan15
kérdése
akosfan15
kérdése
646
Nagyon, nagyon, nagyon örülnék, ha valaki lépésről, lépésre levezetné ezeket a feladatokat!
Jelenleg 1 felhasználó nézi ezt a kérdést.
improprius, integrál, konvergens
improprius, integrál, konvergens
0
Felsőoktatás / Matematika
Válaszok
1 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
1) Mivel a függvény páros, ezért felírható így:
2*int₀∞(1/(x⁴+1)) dx
Az nem nagy varázslat, hogy a [0;1] intervallumon véges. Az [1;∞) intervallumon felülről tudjuk becsülni az 1/x⁴ függvénnyel, erről pedig tudjuk, hogy véges, így az 1/(x⁴+1) is véges lesz.
Véges+véges=véges, 2*véges=véges, tehát az integrál véges lesz.
2) Erre nem tudok (még) egzakt megoldást, de a függvény alulról becsülhető az 1/x függvénnyel, ha x≥94: http://www.wolframalpha.com/input/?i=1%2F(ln(x))%5E3%3E1%2Fx. Az 1/x függvényről tudjuk, hogy nem véges az [1;∞) intervallumon, így értelemszerűen a [94;∞) intervallumon sem lesz véges, és mivel ez alsó becslése az 1/ln³(x)-nek, ezért ennek a végtelenben vett integrálja sem lesz véges.
3) Vonjunk ki a függvényből 3/x³-ont, de adjuk is hozzá, hogy értéke ne változzon, ekkor ezt kapjuk:
int((cos(2x)-sin(x)-3)/x³ dx - int(3/x³) dx
Az első függvény így minden x-re pozitív lesz. Ez a függvény felülről becsülhető -4/x³-bel, erről pedig tudjuk, hogy végtelenben vett integrálja véges. A 3/x³ integrálja is véges, véges-véges=véges.
Ha a másodikra eszembe jut még valami, akkor megírom, de hogy végtelen az integrál, az biztos.
2*int₀∞(1/(x⁴+1)) dx
Az nem nagy varázslat, hogy a [0;1] intervallumon véges. Az [1;∞) intervallumon felülről tudjuk becsülni az 1/x⁴ függvénnyel, erről pedig tudjuk, hogy véges, így az 1/(x⁴+1) is véges lesz.
Véges+véges=véges, 2*véges=véges, tehát az integrál véges lesz.
2) Erre nem tudok (még) egzakt megoldást, de a függvény alulról becsülhető az 1/x függvénnyel, ha x≥94: http://www.wolframalpha.com/input/?i=1%2F(ln(x))%5E3%3E1%2Fx. Az 1/x függvényről tudjuk, hogy nem véges az [1;∞) intervallumon, így értelemszerűen a [94;∞) intervallumon sem lesz véges, és mivel ez alsó becslése az 1/ln³(x)-nek, ezért ennek a végtelenben vett integrálja sem lesz véges.
3) Vonjunk ki a függvényből 3/x³-ont, de adjuk is hozzá, hogy értéke ne változzon, ekkor ezt kapjuk:
int((cos(2x)-sin(x)-3)/x³ dx - int(3/x³) dx
Az első függvény így minden x-re pozitív lesz. Ez a függvény felülről becsülhető -4/x³-bel, erről pedig tudjuk, hogy végtelenben vett integrálja véges. A 3/x³ integrálja is véges, véges-véges=véges.
Ha a másodikra eszembe jut még valami, akkor megírom, de hogy végtelen az integrál, az biztos.
1
- Még nem érkezett komment!