Ez se nem Poisson, se nem exponenciális és nem is binomiális... benne van a szövegben, hogy normál eloszlás.

Az üveg 900 gramos, az azt jelenti, hogy a benne lévő méz várható értéke 900 g. A szórást nem tudjuk.
a)
A normális eloszlásokat gyakorlatilag mindig úgy kell csinálni, hogy a megadott mennyiségeket átalakítjuk standard normális eloszlássá.
A 890 meg a 910 mindkettő 10-zel van odébb a várható értéktől, ezért elég csak az egyikkel számolni. A 910-zel érdemes, mert a standard normális eloszlás táblázata is csak a haranggörbe közepétől nagyobb értékeket tartalmazza.
`x=910`
standardizáltja:
`z_(910)=(x-µ)/σ=(910-900)/σ=10/σ`
Ha ezt ki tudnánk számolni, akkor megnézhetnének a standard normális eloszlás táblázatában, hogy milyen `Φ(z)` érték tartozik hozzá, ami maga a valószínűség, hogy `z`-nél kisebb értékeket vesz fel. Pl. itt van a táblázat:
http://math.bme.hu/~eczirok/dok/2017_18_01/A3/standard_normalis_eloszlas.pdf
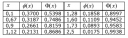
Ami képet adtál, az is részben ebből a táblázatból néhány érték (a `Φ(x)` értékek), viszont csak kevés érték van megadva, nem igazán hasznos ez a táblázat. A kis `φ(x)` értékekről nem is tudom, mik lehetnek. Az valami más eloszlás táblázata lesz...

Szóval nézd inkább a nagy táblázatot, amit linkeltem.
Most valamilyen valószínűséget ismerünk, tehát visszafelé tudjuk használni a táblázatot, a valószínűségből tudjuk visszakeresni, hogy milyen `z` értékhez tartozik.
De a táblázat nem olyan valószínűséget tartalmaz, mint ami nekünk van. Nekünk az van, hogy a haranggörbe csúcsa körül `+-10` illetve standardizálva `+-z` tartományon KÍVÜL mi a valószínűség. A tartományon belül `1-"0,1096"="0,8904"` a valószínűség. Annak a fele van a csúcsnál nagyobb értékeknél, a másik fele meg a csúcsnál kisebb értékeknél. (Tiszta? Képzeld el a haranggörbét.)
Vagyis a csúcsnál nagyobb féltartománynak a valószínűsége `"0,8904"/2="0,4452`
A mínusz végtelentől a csúcsig terjedő tartománynak, tehát a haranggörbe felének a valószínűsége `"0,5"`. Ahhoz adódik még a `"0,4452`, tehát annak a valószínűsége, hogy 910-nél (standardizált `z`-nél) kevesebb méz megy az üvegbe, az `"0,9452"`.

A táblázatban pont az ilyen `P(ξ < z)` valószínűségek vannak. A `z_(910)` standardizált értékhez a `"0,9452"` valószínűség tartozik. Mázlink van, van pontosan `"0,9452"` érték még a kis táblázatban is, nem kell interpolálnunk: `z="1,60"` értékhez tartozik ez a valószínűség.
`z_(910)="1,6"`
`10/σ="1,6"`
Ebből már kijön a szórás, 6,25.

b)
Most azt mondja a feladat, hogy nem biztos, hogy normális eloszlásunk van, lehet bármi. Olyankor nem használhatjuk a normális eloszlás táblázatát, hanem a sokkal durvább Csebisev egyenlőtlenség használható csak.
`P(|X-µ| ≥ k) ≤ σ^2/k^2`
ami azt jelenti, hogy annak a valószínűsége, hogy a várható érték (`µ`) körüli `k` sugarú tartományon kívül esik az érték (`X`), az kisebb, mint `σ^2/k^2`.
Most `k=10`, hisz 900 körüli `+-10` tartományon kívüli valószínűséget keresünk.
Behelyettesítve a `k`-t meg az ismert valószínűséget:
`"0,1096" ≤ σ^2/100`
Ebből 10.47-es szórás jön ki. (Látszik, hogy ha ismerjük az eloszlást, akkor sokkal pontosabb becslést tudunk adni.)