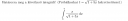Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Helyettesítéses integrál
Cintikra
kérdése
292
Mellékelem képen a feladatot! Köszönöm.
Jelenleg 1 felhasználó nézi ezt a kérdést.
integrál, integrálás, Matematika, analízis, helyettesítésesintegrál
integrál, integrálás, Matematika, analízis, helyettesítésesintegrál
0
Felsőoktatás / Matematika
Válaszok
1
AlBundy
{ Polihisztor }
megoldása
Ha `t=sqrt(1+5x)`, akkor `x=(t^2-1)/5` és `(dt)/(dx)=5/(2sqrt(1+5x))`, vagyis `dt=5/(2sqrt(1+5x)) dx`. Ezekből át tudjuk írni az integrandust `t` szerint:
`x/sqrt(1+5x) dx=2/5*x*dt=2/5*(t^2-1)/5*dt=2/25 (t^2-1) dt`
Tehát az integrál:
`int_3^7 x/sqrt(1+5x) dx``=``int_{sqrt(1+5*3)}^{sqrt(1+5*7)} 2/25 (t^2-1) dt``=``2/25 int_4^6 (t^2-1) dt``=``2/25 [t^3/3-t]_4^6``=``2/25(216/3-6-64/3+4)=292/75`
Ellenőrzés: https://www.wolframalpha.com/input/?i=int%28x%2Fsqrt%281%2B5x%29%2C+x%2C+3%2C+7%29
`x/sqrt(1+5x) dx=2/5*x*dt=2/5*(t^2-1)/5*dt=2/25 (t^2-1) dt`
Tehát az integrál:
`int_3^7 x/sqrt(1+5x) dx``=``int_{sqrt(1+5*3)}^{sqrt(1+5*7)} 2/25 (t^2-1) dt``=``2/25 int_4^6 (t^2-1) dt``=``2/25 [t^3/3-t]_4^6``=``2/25(216/3-6-64/3+4)=292/75`
Ellenőrzés: https://www.wolframalpha.com/input/?i=int%28x%2Fsqrt%281%2B5x%29%2C+x%2C+3%2C+7%29
0
- Még nem érkezett komment!