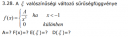Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valószínűségszámítás|Eloszlás, eloszlásfüggvény, sűrűségfüggvény|2. és 3. feladat képként csatolva!
 CiscoM
kérdése
CiscoM
kérdése
468
1.feladat
Egy dobozban van 5 piros és 15 fehér golyó. Kiveszünk 6 darabot, mi a
valószínűsége, hogy 4 piros lesz köztük, ha
a) visszatevés nélkül húzunk?
b) visszatevéssel húzunk?
c) mi a helyzet, ha 1 piros és 3 fehér illetve, ha 100 piros és 300 fehér van?
2.feladat
A második feladatot képként csatoltam!
3.feladat
A harmadik feladatot képként csatoltam!
Egy dobozban van 5 piros és 15 fehér golyó. Kiveszünk 6 darabot, mi a
valószínűsége, hogy 4 piros lesz köztük, ha
a) visszatevés nélkül húzunk?
b) visszatevéssel húzunk?
c) mi a helyzet, ha 1 piros és 3 fehér illetve, ha 100 piros és 300 fehér van?
2.feladat
A második feladatot képként csatoltam!
3.feladat
A harmadik feladatot képként csatoltam!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
1.
a) Visszatevés nélkül, vagyis `bb"hipergeometrikus"` eloszlás.
`N=20` golyó összesen
`M=5` piros
`n=6` húzottak száma
`k=4` lesz az `M` közül:
`P(X=k)=( ((M),(k)) · ((N-M),(n-k)) )/( ((N),(n)) )`
ami úgy jön ki, hogy:
Összes esetek száma `((N),(n))`, ennyiféleképpen választhatunk ki `n` darabot.
Kedvező esetek száma: az `M` közül választunk `k` darabot ( `((M),(k))` ) és a maradékből a maradékot (`((N-M),(n-k))`).
Helyettesíts be.
b) Visszatevéssel, vagyis `bb"binomiális"` eloszlás.
`p=5/20` a piros húzás valószínűsége
`n=6` húzottak száma
`k=4` lesz piros:
`P(X=k)=((n),(k))p^k (1-p)^(n-k)`
ami úgy jön ki, hogy:
Az `n` húzás közül `((n),(k))` helyen lehet az, ahol pirosat húzunk. `k` alkalommal pirosat húzunk `p^k` valószínűséggel, a többi `n-k` alkalommal pedig fehé√et `(1-p)^(n-k)` valószínűséggel.
Helyettesíts be.
c)
1 piros és 3 fehérből csak visszatevéssel tudunk 6-szor húzni, szóval bioznyára visszatevéses húzásról van szó. Akkor pedig nincs különbség a kettő között, mert `p=1/4=100/400` egyforma.
a) Visszatevés nélkül, vagyis `bb"hipergeometrikus"` eloszlás.
`N=20` golyó összesen
`M=5` piros
`n=6` húzottak száma
`k=4` lesz az `M` közül:
`P(X=k)=( ((M),(k)) · ((N-M),(n-k)) )/( ((N),(n)) )`
ami úgy jön ki, hogy:
Összes esetek száma `((N),(n))`, ennyiféleképpen választhatunk ki `n` darabot.
Kedvező esetek száma: az `M` közül választunk `k` darabot ( `((M),(k))` ) és a maradékből a maradékot (`((N-M),(n-k))`).
Helyettesíts be.
b) Visszatevéssel, vagyis `bb"binomiális"` eloszlás.
`p=5/20` a piros húzás valószínűsége
`n=6` húzottak száma
`k=4` lesz piros:
`P(X=k)=((n),(k))p^k (1-p)^(n-k)`
ami úgy jön ki, hogy:
Az `n` húzás közül `((n),(k))` helyen lehet az, ahol pirosat húzunk. `k` alkalommal pirosat húzunk `p^k` valószínűséggel, a többi `n-k` alkalommal pedig fehé√et `(1-p)^(n-k)` valószínűséggel.
Helyettesíts be.
c)
1 piros és 3 fehérből csak visszatevéssel tudunk 6-szor húzni, szóval bioznyára visszatevéses húzásról van szó. Akkor pedig nincs különbség a kettő között, mert `p=1/4=100/400` egyforma.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
3.28.
a) `A=?`
Akkor sűrűségfüggvény egy `f(x)` függvény, ha `int_(-∞)^∞\ f(x)\ dx = 1`. Ennek most is teljesülnie kell. Mivel -1 fölött nulla az érték, csak -1-ig kell integrálni:
`int_(-∞)^(-1)\ A/x^3\ dx = [-A/(2x^2) ]_(-∞)^(-1)=-A/2-0=1`
`A=-2`
b) `F(x)=?`
`x` helyett ideiglenesen nevezzük mondjuk `t`-nek, hogy ne kavarodjon a másik `x`-szel:
`F(t)=int_(-∞)^tf(x)\ dx=int_(-∞)^t(-2)/x^3\ dx=[1/(x^2) ]_(-∞)^(t)=1/t^2`
Ez a képlet `t < -1` esetén igaz, fölötte már a nullát kell hozzá-integrálni.
vagyis
`F(x)={(1/x^2,"ha",x < -1),(1, , "különben"):}`
c) `E(ξ)=?`
`E(ξ)=int_(-∞)^∞\ x·f(x)\ dx`
amit megint csak -1-ig kell integrálni (hisz fölötte nulla)
`=int_(-∞)^(-1)\ x·(-2)/x^3\ dx=[2/x]_(-∞)^(-1)=-2`
d) `D(ξ)=?`
`D^2(ξ)=E(ξ^2)-E^2(ξ)=E(ξ^2)-4`
`E(ξ^2)=int_(-∞)^∞\ x^2·f(x)\ dx`
megint csak -1-ig:
`=int_(-∞)^(-1)\ x^2·(-2)/x^3\ dx=[-2\ "ln"(x)]_(-∞)^(-1)`
Se `"ln"("-1")`, se `"ln"("-∞")` nem létezik a valós számok halmazán, ezért nincs szórás!
a) `A=?`
Akkor sűrűségfüggvény egy `f(x)` függvény, ha `int_(-∞)^∞\ f(x)\ dx = 1`. Ennek most is teljesülnie kell. Mivel -1 fölött nulla az érték, csak -1-ig kell integrálni:
`int_(-∞)^(-1)\ A/x^3\ dx = [-A/(2x^2) ]_(-∞)^(-1)=-A/2-0=1`
`A=-2`
b) `F(x)=?`
`x` helyett ideiglenesen nevezzük mondjuk `t`-nek, hogy ne kavarodjon a másik `x`-szel:
`F(t)=int_(-∞)^tf(x)\ dx=int_(-∞)^t(-2)/x^3\ dx=[1/(x^2) ]_(-∞)^(t)=1/t^2`
Ez a képlet `t < -1` esetén igaz, fölötte már a nullát kell hozzá-integrálni.
vagyis
`F(x)={(1/x^2,"ha",x < -1),(1, , "különben"):}`
c) `E(ξ)=?`
`E(ξ)=int_(-∞)^∞\ x·f(x)\ dx`
amit megint csak -1-ig kell integrálni (hisz fölötte nulla)
`=int_(-∞)^(-1)\ x·(-2)/x^3\ dx=[2/x]_(-∞)^(-1)=-2`
d) `D(ξ)=?`
`D^2(ξ)=E(ξ^2)-E^2(ξ)=E(ξ^2)-4`
`E(ξ^2)=int_(-∞)^∞\ x^2·f(x)\ dx`
megint csak -1-ig:
`=int_(-∞)^(-1)\ x^2·(-2)/x^3\ dx=[-2\ "ln"(x)]_(-∞)^(-1)`
Se `"ln"("-1")`, se `"ln"("-∞")` nem létezik a valós számok halmazán, ezért nincs szórás!
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
3.32.
Az eloszlásfüggvénynek van néhány tulajdonsága:
- Monoton nől, ez teljesül az adott függvényre
- Határértéke -∞-ben 0, ez is OK
- Határértéke +∞-ben 1, ez viszont nem teljesül! Már x=1-ben az értéke 1 lesz, és utána tovább nől 2-ig.
Tehát ez nem lehet eloszlásfüggvény.
Az eloszlásfüggvénynek van néhány tulajdonsága:
- Monoton nől, ez teljesül az adott függvényre
- Határértéke -∞-ben 0, ez is OK
- Határértéke +∞-ben 1, ez viszont nem teljesül! Már x=1-ben az értéke 1 lesz, és utána tovább nől 2-ig.
Tehát ez nem lehet eloszlásfüggvény.
0
- Még nem érkezett komment!