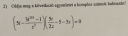Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika
 t.robi01195
kérdése
t.robi01195
kérdése
437
Oldja meg a következő egyenletet a komplex számok halmazán.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A szorzat akkor lehet nulla, ha valamelyik tényezője nulla. Nézzük az első tényezőt:
`5i - (3i^255-1)/z^2=0`
Először is tudjuk, hogy `i`-nek minden 4-gyel osztható hatványa 1, tehát `i^255``=``i^252*i^2*i``=``1*(-1)*i``=``-i`. Innen:
`5i - (-3i-1)/z^2=0`
Szorozzunk be `z^2`-tel:
`5iz^2 - (-3i-1)=0`
`z^2=(-3i-1)/(5i)`
Bővítsük a törtet `i`-vel:
`z^2=(3-i)/(-5)=(i-3)/5`
Ennek a számnak az abszolút értéke `sqrt(10)/5`, szöge `pi-\text{arctg}1/3`, tehát:
`z^2=sqrt(10)/5 e^(i(pi-\text{arctg}1/3))`
Ennek a gyökei adják az első két megoldást:
`z_1=sqrt(sqrt(10)/5) e^(i(pi/2-1/2\text{arctg}1/3))~~0.7953 e^(1.41i)~~0.1274 + 0.7850i`
`z_2=-z_1~~0.7953 e^(-1.73i)~~- 0.1274 - 0.7850i`
Nézzük a második tényezőt:
`(5i)/(2z)-5-3z=0`
Szorozzunk be `2z`-vel:
`5i-10z-6z^2=0`
`6z^2+10z-5i=0`
Használjuk a másodfokú egyenlet megoldóképletét:
`z_{3,4}=(-10 pm sqrt(100-4*6*(-5i)))/12=(-5 pm sqrt(25+30i))/6`
Ezek is csúnya számok, a kerekített értékek:
`z_3~~ 0.1099 + 0.4418i`
`z_4~~ -1.7765 - 0.4418i`
Ellenőrzés: https://www.wolframalpha.com/input/?i=%285i+-+%283i%5E255-1%29%2Fz%5E2%29%28%285i%29%2F%282z%29-5-3z%29%3D0
`5i - (3i^255-1)/z^2=0`
Először is tudjuk, hogy `i`-nek minden 4-gyel osztható hatványa 1, tehát `i^255``=``i^252*i^2*i``=``1*(-1)*i``=``-i`. Innen:
`5i - (-3i-1)/z^2=0`
Szorozzunk be `z^2`-tel:
`5iz^2 - (-3i-1)=0`
`z^2=(-3i-1)/(5i)`
Bővítsük a törtet `i`-vel:
`z^2=(3-i)/(-5)=(i-3)/5`
Ennek a számnak az abszolút értéke `sqrt(10)/5`, szöge `pi-\text{arctg}1/3`, tehát:
`z^2=sqrt(10)/5 e^(i(pi-\text{arctg}1/3))`
Ennek a gyökei adják az első két megoldást:
`z_1=sqrt(sqrt(10)/5) e^(i(pi/2-1/2\text{arctg}1/3))~~0.7953 e^(1.41i)~~0.1274 + 0.7850i`
`z_2=-z_1~~0.7953 e^(-1.73i)~~- 0.1274 - 0.7850i`
Nézzük a második tényezőt:
`(5i)/(2z)-5-3z=0`
Szorozzunk be `2z`-vel:
`5i-10z-6z^2=0`
`6z^2+10z-5i=0`
Használjuk a másodfokú egyenlet megoldóképletét:
`z_{3,4}=(-10 pm sqrt(100-4*6*(-5i)))/12=(-5 pm sqrt(25+30i))/6`
Ezek is csúnya számok, a kerekített értékek:
`z_3~~ 0.1099 + 0.4418i`
`z_4~~ -1.7765 - 0.4418i`
Ellenőrzés: https://www.wolframalpha.com/input/?i=%285i+-+%283i%5E255-1%29%2Fz%5E2%29%28%285i%29%2F%282z%29-5-3z%29%3D0
0
-
t.robi01195: Csak egy kérdésem lenne. A végén hogy kapom azokat a kerekített számokat z3 és z4-re ? 6 éve 0
-
AlBundy: Jobb híján számológéppel. Ha a számológéped nem tud gyököt vonni komplex számból, akkor ki kell számolnod a trigonometrikus alakot, és megcsinálni a gyökvonást úgy, ahogy az első két megoldásnál. `25+30i` abszolút értéke `5sqrt(61)`, szöge `\text{arctg}(1.2)`, tehát `25+30i=5sqrt(61) e^(i*\text{arctg}(1.2))`. 6 éve 0
-
AlBundy: Innen a gyökök `sqrt(25+30i)``=``pm sqrt(5sqrt(61))e^(i*1/2 \text{arctg}(1.2))``=``pm (sqrt(5sqrt(61)) cos(1/2 \text{arctg}(1.2))+i* sqrt(5sqrt(61))sin(1/2 \text{arctg}(1.2)))``~~``pm(5.6591+i2.6506)`. 6 éve 0
-
AlBundy: És akkor a végeredmény `z_{3,4}~~(-5 pm (5.6591+i2.6506))/6`, ez pedig már tiszta sor. 6 éve 0