Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Diszkrét matematika: Ford-Fulkerson alg.
t.robi01195
kérdése
279
A kérdés a következő lenne egy diszkrét matek vizsgán:
3.
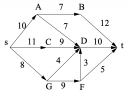
a, A Ford-Fulkerson algoritmussal határozza meg a maximális folyamot az
alábbi hálózatban! Az első javító útnak válassza az s − A − D − t utat! Az
algoritmus lépéseit is írja le!
b, Adjon meg egy minimális vágást!
c, Mennyi az (s, A, B) vágás értéke?
3.
a, A Ford-Fulkerson algoritmussal határozza meg a maximális folyamot az
alábbi hálózatban! Az első javító útnak válassza az s − A − D − t utat! Az
algoritmus lépéseit is írja le!
b, Adjon meg egy minimális vágást!
c, Mennyi az (s, A, B) vágás értéke?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1
AlBundy
{ Polihisztor }
megoldása
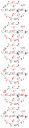
Induljunk csupa nulla folyamból. Az algoritmus egy lehetséges futása az alábbi, a fokozatos javításokról mellékeltem képet.
1. javító út: sADt, a folyam értéke 7.
2. javító út: sABt, a folyam értéke 10.
3. javító út: sGFt, a folyam értéke 15.
4. javító út: sGFDt, a folyam értéke 18.
5. javító út: sCDABt, a folyam értéke 22.
Rögtön látszik, hogy ez a folyam már maximális, ugyanis teljesen kihasználja a nyelőbe befutó élek kapacitásait (B-nél nincs elágazás, ezért az AB és Bt élek lényegében összevonhatók 7-es kapacitással).
Minimális (tehát 22 értékű) vágás például az {s, A, C, D, F, G}, {B, t} partíció, azaz ha az AB, Dt, Ft élek mentén vágjuk fel a gráfot.
A c) kérdést úgy kell érteni, hogy a vágás egyik részét az {s, A, B}, a másikat pedig a {C, D, F, G, t} pontok alkotják? Ha igen, akkor a gráfot az sG, sC, AD, Bt élek mentén vágtuk fel, tehát a vágás értéke `8+11+7+12=38`.
1. javító út: sADt, a folyam értéke 7.
2. javító út: sABt, a folyam értéke 10.
3. javító út: sGFt, a folyam értéke 15.
4. javító út: sGFDt, a folyam értéke 18.
5. javító út: sCDABt, a folyam értéke 22.
Rögtön látszik, hogy ez a folyam már maximális, ugyanis teljesen kihasználja a nyelőbe befutó élek kapacitásait (B-nél nincs elágazás, ezért az AB és Bt élek lényegében összevonhatók 7-es kapacitással).
Minimális (tehát 22 értékű) vágás például az {s, A, C, D, F, G}, {B, t} partíció, azaz ha az AB, Dt, Ft élek mentén vágjuk fel a gráfot.
A c) kérdést úgy kell érteni, hogy a vágás egyik részét az {s, A, B}, a másikat pedig a {C, D, F, G, t} pontok alkotják? Ha igen, akkor a gráfot az sG, sC, AD, Bt élek mentén vágtuk fel, tehát a vágás értéke `8+11+7+12=38`.
Módosítva: 4 éve
0
- Még nem érkezett komment!