Mivel `A rightarrow B` esetén izoterm folyamatról van szó, akkor
`W_(AB)=-frac{m}{M}RT_A*ln(frac{V_B}{V_A})` valamint `U_(AB)=Delta U=0`.

Továbbá `B rightarrow C` esetén `U_(BC)=-Delta U=-W_(BC)`, mert
itt adiabatikus a folyamat;
`C rightarrow D` esetén `U_(CD)=Delta U=0`, megint izotermáról beszélünk;
végül `C rightarrow D` esetén `U_(DA)=+Delta U=W_(DA)` megint adiabata.
Így a teljes belső energia megváltozás zérus.

Lásd még: en.wikipedia.org/wiki/Carnot_cycle
hu.wikipedia.org/wiki/Carnot-ciklus

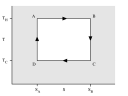
`T_H=T_1=T_2`; `T_C=T_3=T_4`.
(H-hot; C-cold)
(szokták még alkalmazni `Q_(fel)=Q_1` ill. `Q_(text(le))=Q_2` jelöléseket is)
`Q_1=W_(AB)`
és mivel `Q_1-Q_2=W_(AB)-W_(CD)-W_(DA)+W_(BC)=W`
ahol `W` a rendszer munkája.
Ezért `Q_2=W_(CD)+W_(DA)-W_(BC)`
Természetesen `Q_1 gt Q_2` .
Ebből a hatásfok `eta=frac{W}{Q_1}=frac{Q_1-Q_2}{Q_1}`,
azt mutatja meg, hogy a forró hőtartályból felvett hő hányadrészét alakítják munkává.

Tudjuk, hogy állandó nyomáson a dugattyúra állandó
`F=p*A` erővel kell hatni. A végzett munka `W=pA*s` és az egyik geometriai összefüggés
alapján `W=-p*Delta V`,
itt figyelembe vettük az előjelválasztást. Ábrázolva a nyomást a térfogat függvényében
felírhatunk egy integrálközelítő összeget a munkára:
`p_1*frac{Delta V}{n}+p_2*frac{DeltaV}{n}+...+p_n*frac{DeltaV}{n}`
Ennek határértéke `W=-int_(V_1)^(V_2) p(V) dV` térfogati integrál.

Állandó hőmérsékleten az egyesített gáztörvényből
`p(V)=frac{p_1*V_1}{V}` függvényt integrálva a megadott tartományon,
kapjuk az izoterm munkát `W=-frac{m}{M}*R*T_C*ln(frac{V_2}{V_1})`.

Teljesen hőszigetelt rendszerben a nyomás az adiabata egyenlete alapján számítható:
Vegyük fel a `p(V)=p_1*(frac{V_1}{V})^(kappa)` függvényt és integráljunk
a megadott tartományon. Eredményünk `W=frac{p_1*V_1-p_2*V_2}{1-kappa}` lesz.

Kiegészítésül az érintett folyamatokra igaz lesz még:
`A rightarrow B` esetén `Q_(AB)=Q_1`,
`B rightarrow C` esetén `Q_(BC)=0` és a fenti adibata munkaképletet
alkalmazva `W_(BC)=frac{p_C*V_C-p_B*V_B}{kappa-1}`
továbbá `C rightarrow D` esetén `Q_(CD)=-Q_2` és fenti izoterm munka
képletet alkalmazva
`W_(CD)=-frac{m}{M}*R*T_C*ln(frac{V_D}{V_C})`.
Befejezésül `D rightarrow A` esetén `Q_(DA)=0` és
`W_(DA)=frac{p_A*V_A-p_D*V_D}{kappa-1}`.

(Megjegyzés: A sárga függvénytáblázat egyes kiadásainál a Carnot-körfolyamat
leírásánál olyan elírás vehető észre, ahol fordítva szerepel a hőmérséklet indexe
és e miatt negatív hatásfokot kapnánk.
Természetesen minden esetben a hatásfok nemnegatív értéket vehet fel.)

Ideális gázzal működő Carnot-féle körfolyamat hatásfoka:

`eta_(id)=1-frac{T_2}{T_1}` .

Bizonyítás:

Felhasználva, hogy `p_A*V_A+p_C*V_C=p_B*V_B+p_D*V_D` azonosságot
és az izotermikus folyamat alatt végzett munkák hányadosa
`frac{W_(CD)}{W_(AB)}=frac{Q_2}{Q_1}=frac{Q_(text(le))}{Q_(fel)}=`
`=-frac{frac{m}{M}*R*T_2*ln(frac{V_D}{V_C})}{frac{m}{M}*R*T_1*ln(frac{V_B}{V_A})}`.


Továbbá felhasználva az adiabatákra vonatkozó egyenleteket

`T_1*V_B^(kappa-1)=T_2*V_C^(kappa-1)`
`T_1*V_A^(kappa-1)=T_2*V_D^(kappa-1)`

elosztva a kétegyenletet egymással és `(kappa-1)`-edik gyököt vonva kapjuk, hogy
`frac{V_D}{V_C}=frac{V_A}{V_B}`
Ezt viszzahelyettesítve a fenti logaritmusos egyenletbe kapjuk az ideális gázokra
vonatkozó `eta_(id)` hatásfokot.

Végezetül néhány gondolat az entrópiáról.

`frac{Q_1}{T_1}+frac{Q_2}{T_2}=frac{W_(AB)}{T_1}+frac{W_(CD)}{T_2}=`

`=frac{m*R}{M}*(frac{T_A}{T_1}*ln(frac{V_B}{V_A})+frac{T_C}{T_2}*ln(frac{V_D}{V_C}))=`

`=frac{m*R}{M}*ln(frac{V_B*V_D}{V_A*V_C})=0`.

vagyis a Carnot-körfolyamat esetén a redukált hőmennyiségek vagy entrópiák
összege zérus: `S_1+S_2=0`, ahol `S_1=frac{Q_1}{T_1}` ill. `S_2=frac{Q_2}{T_2}`.