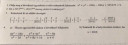Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki segítsen, nagyon köszönöm!
 Törölt
kérdése
Törölt
kérdése
2368
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4 bongolo
{
bongolo
{  }
megoldása
}
megoldása
1.
Azt lehet sejteni, hogy teljes négyzetet talán érdemes csinálni.
258=2·129, 846=2·423, vagyis ilyen teljes négyzetek lehetnek benne: `(x-129)^2` és `(y-423)^2`
`(x-129)^2=x^2-258x+129^2=x^2-258x+16641`
`(y-423)^2=y^2-846y+423^2=y^2-846y+178929`
Ezek összege:
`(x-129)^2+(y-423)^2=x^2+y^2-258x-846y+195570`
Mázlink van, ez éppen a megoldandó egyenlet bal oldala. Vagyis ez az egyenlet:
`(x-129)^2+(y-423)^2=0`
Innen meg tudod oldani? Egyetlen trükkre kell rájönni. Ha nem ugrik be, szólj.
Azt lehet sejteni, hogy teljes négyzetet talán érdemes csinálni.
258=2·129, 846=2·423, vagyis ilyen teljes négyzetek lehetnek benne: `(x-129)^2` és `(y-423)^2`
`(x-129)^2=x^2-258x+129^2=x^2-258x+16641`
`(y-423)^2=y^2-846y+423^2=y^2-846y+178929`
Ezek összege:
`(x-129)^2+(y-423)^2=x^2+y^2-258x-846y+195570`
Mázlink van, ez éppen a megoldandó egyenlet bal oldala. Vagyis ez az egyenlet:
`(x-129)^2+(y-423)^2=0`
Innen meg tudod oldani? Egyetlen trükkre kell rájönni. Ha nem ugrik be, szólj.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
2.
`2015^2015+2015^2016=(1+2015)·2015^2015`
Nézzük a prímfelbontásokat:
`2015=5·13·31`
`2016=2^5·3^2·7`
Vagyis a szorzat prímtényezői ezek:
`2016·2015^2015=(2^5·3^2·7)·(5^2015·13^2015·31^2015)`
Mivel a 2016-ban benne van a `2^5`, a `2015^2015`-ben pedig `5^2015` (amiből elég lenne most az `5^5` is), a szorzatuk osztható lesz `10^5`-nel. Vagyis az utolsó 5 számjegy tuti nulla!
Ha elhagyjuk a szorzatból a `10^5`-t, ennyi marad:
`3^2·7·5^2010·13^2015·31^2015`
Ez páratlan és osztható 5-tel. Ezért ez a szám 5-re végződik.
Tehát a teljes szám utolsó 6 számjegye `500000`
`2015^2015+2015^2016=(1+2015)·2015^2015`
Nézzük a prímfelbontásokat:
`2015=5·13·31`
`2016=2^5·3^2·7`
Vagyis a szorzat prímtényezői ezek:
`2016·2015^2015=(2^5·3^2·7)·(5^2015·13^2015·31^2015)`
Mivel a 2016-ban benne van a `2^5`, a `2015^2015`-ben pedig `5^2015` (amiből elég lenne most az `5^5` is), a szorzatuk osztható lesz `10^5`-nel. Vagyis az utolsó 5 számjegy tuti nulla!
Ha elhagyjuk a szorzatból a `10^5`-t, ennyi marad:
`3^2·7·5^2010·13^2015·31^2015`
Ez páratlan és osztható 5-tel. Ezért ez a szám 5-re végződik.
Tehát a teljes szám utolsó 6 számjegye `500000`
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
3.
Írjuk fel őket külön sorokba, egymás alá az azonos nevezőjűeket:
`{:
(-1/2,+1/3,-1/4,+1/5,...,-1/2018),
( ,+2/3,-2/4,+2/5,...,-2/2018),
( , ,-3/4,+3/5,...,-3/2018),
( , , ,+4/5,...,-4/2018),
( , , , ,..., ...),
( , , , , ,-2017/2018)
:}`
Aztán adjuk össze függőlegesen.
Páratlanadik oszlop negatív, párosadik pedig pozitív. Az `n`-edik oszlopban 1-től `n`-ig vannak összeadva a növekvő számok, és ez az összeg `n+1`-gyel van osztva. A számláló egy számtani sorozat összege:
`S_n=(n·(n+1))/2`
Mivel ez `n+1`-gyel van osztva, az `n`-edik oszlop összege `n/2` (megfelelő előjellel).
Végül az oszlopok összegének az összege ez lesz:
`-1/2+2/2-3/2+4/2-5/2+6/2-...+2016/2-2017/2`
Ha ezt kettesével zárójelezem:
`(-1/2+2/2)+(-3/2+4/2)+(-5/2+6/2)+...+(-2015/2+2016/2)-2017/2`
Az utolsónak nem volt párja... Összesen lett `2016/2` darab zárójeles összeg plusz egy önálló tört.
Mindegyik zárójelesnek az összevont értéke ... fejezd be. Ha kell segítség,. szólj.
Írjuk fel őket külön sorokba, egymás alá az azonos nevezőjűeket:
`{:
(-1/2,+1/3,-1/4,+1/5,...,-1/2018),
( ,+2/3,-2/4,+2/5,...,-2/2018),
( , ,-3/4,+3/5,...,-3/2018),
( , , ,+4/5,...,-4/2018),
( , , , ,..., ...),
( , , , , ,-2017/2018)
:}`
Aztán adjuk össze függőlegesen.
Páratlanadik oszlop negatív, párosadik pedig pozitív. Az `n`-edik oszlopban 1-től `n`-ig vannak összeadva a növekvő számok, és ez az összeg `n+1`-gyel van osztva. A számláló egy számtani sorozat összege:
`S_n=(n·(n+1))/2`
Mivel ez `n+1`-gyel van osztva, az `n`-edik oszlop összege `n/2` (megfelelő előjellel).
Végül az oszlopok összegének az összege ez lesz:
`-1/2+2/2-3/2+4/2-5/2+6/2-...+2016/2-2017/2`
Ha ezt kettesével zárójelezem:
`(-1/2+2/2)+(-3/2+4/2)+(-5/2+6/2)+...+(-2015/2+2016/2)-2017/2`
Az utolsónak nem volt párja... Összesen lett `2016/2` darab zárójeles összeg plusz egy önálló tört.
Mindegyik zárójelesnek az összevont értéke ... fejezd be. Ha kell segítség,. szólj.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
4.
Most amit csak lehet, szorzattá kell alakítani:
`4x^2-16x=4x(x-4)`
`x^2-16=(x-4)(x+4)`
Ezek hányadosa egyszerűsítés után `(4x)/(x+4)`
`x^3+4x^2=x^2(x+4)`
`x^2+8x+16=(x+4)^2`
Ezek hányadosa egyszerűsítés után `(x^2)/(x+4)`
`x^2-8x=x(x-8)`
`x+4` nem lehet szorzattá alakítani
A harmadiknak a hányadosánál se lehet egyszerűsíteni.
Lehet, hogy a harmadik számlálóját se volt érdemes szorzattá lakítani... majd kiderül.
Szerencsére mindegyiknek ugyanaz lett a nevezője, vagyis a három törtet össze lehet vonni.
Vond össze, kiesik sok minden.
Fejezd be. A b) pontot se felejtsd el!
Most amit csak lehet, szorzattá kell alakítani:
`4x^2-16x=4x(x-4)`
`x^2-16=(x-4)(x+4)`
Ezek hányadosa egyszerűsítés után `(4x)/(x+4)`
`x^3+4x^2=x^2(x+4)`
`x^2+8x+16=(x+4)^2`
Ezek hányadosa egyszerűsítés után `(x^2)/(x+4)`
`x^2-8x=x(x-8)`
`x+4` nem lehet szorzattá alakítani
A harmadiknak a hányadosánál se lehet egyszerűsíteni.
Lehet, hogy a harmadik számlálóját se volt érdemes szorzattá lakítani... majd kiderül.
Szerencsére mindegyiknek ugyanaz lett a nevezője, vagyis a három törtet össze lehet vonni.
Vond össze, kiesik sok minden.
Fejezd be. A b) pontot se felejtsd el!
0
- Még nem érkezett komment!