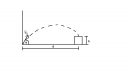
Ferde hajítás (kép csatolva)

Számold ki a sebesség vízszintes és függőleges komponensét:
`v_(0v)=v_0·cos\ α`
`v_(0f)=v_0·sin\ α`
A vízszintes sebesség mindig ennyi marad, a függőleges pedig csökken aztán nő...

A vízszintes mozgás a vízszintes sebességtől függ. Ha összesen `d` távolságra jut `t` idő alatt, akkor `d=v_(0v)·t`. Ebből kijön az idő. (Persze a sebességet m/s-ba át kell váltani.)

A függőleges kezdősebességből pedig kijön a függőleges mozgás. `t` idő alatt felemelkedik, aztán leesik éppen `h` magasságra:
`h=v_(0f)·t-1/2·g·t^2`

A végén a test sebességét energiamegmaradással lehet kiszámolni:
`1/2·m·v_0^2=m·g·h+1/2·m·v^2`
(kiesik a tömeg)

-----------------------------------------------------------

Ahogy kazah írta, sok megoldás lehet az épület alakjától függően. Ha pl. kocka alakú az épület és pont a közepére esik a tárgy, akkor lehet ugyanúgy számolni, ahogy fentebb írtam, csak `d=150\ m` olyankor, vagyis az épület közepének a távolsága.

`t=d/v_(0v)=(150\ m)/(25\ m/s)=6\ s`
`h=v_(0f)·t-1/2·g·t^2=43.3 m/s·6\ s-5 m/s^2·36\ s^2=259.8\ m-180\ m=79.8\ m`

Ez baromi magas épület, hmm... kb. 30-35 emelet.

Egyáltalán nem biztos, hogy kocka alakú az épület...

v = 180 `(km)/h` = 50 `m/s`

`alpha` = 60°

d = 100 m

Felbontjuk a sebességet vízszintes és függőleges komponensre:

`v_x` = `v*cosalpha` = `50*cos60` = 25 `m/s`

`v_y` = `v*sinalpha` = `50*sin60` = 43,3 `m/s`

Mennyi ideig tartózkodik a levegőben a test?

Ezt a függőleges irányú mozgása dönti el, aminek a gyorsulását, lassulását a szabadesés határozza meg.

A vízszintes irányú mozgása egyenletes, mindig `v_x` = 25 `m/s`-mal történik.

Vízszintesen d=100 m-t megtesz t = `d/v_x` = `100/25` = 4 s múlva. (és már meg is tudtuk, mennyi ideig repül a test).

A test felfelé megy:

`v_y` = `g*t_1`

`t_1`= `v_y/g` = 4.3 s-ig.

Ebből kiderült, hogy a felfelé szálló ágon lesz az épület felett a test. (Mondjuk így nem tud rá le-esni, hiszen fel-felé megy.) Ebből az is kiderült, hogy a test nem d távolságra fog becsapódni, csak a d távolságra levő épület tetején. Így aztán elég sok megoldás lehetséges, mert az épületnek van kiterjedése, ha pl 200 m hosszú az épület, akkor lehet akár 1 m magas is, a tetején fog becsapódni.

4 s alatt a test felfelé megtesz

`v_(0y)` = `v_y` - `g*t` = 43,3-`10*4` = 3,3 `m/s`

h = `v_y*t`-`g/2*t^2` = `43.3*4`-`10/2*4^2` = 173,2-80 = 93,2 m

(Ennyi a maximális magasság, ennél kisebb is lehet, ha elég széles). Ha úgy van a d távolság, ahogy a képen látható, akkor a test vagy eltalálja az oldalát vagy elszáll a messzeségbe...

Ebben a magasságban a test sebessége (akár lefelé, akár felfelé megy):

v = `root()(v_x^2+v_(0y)^2)` = `root()(25^2+3.3^2)` = 25,22 `m/s`

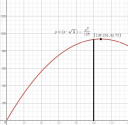
Ahogy az ábrán is látható, a test 100 m-nél felfelé ível, így ha a közepétől mérjük az épület távolságát, akkor nem fog ráesni.

x = `50*t*cos60`

t = `x/(50*cos60)` = `x/25`

y = `50*t*sin60` - `g/2*t^2`

y = `50*root()(3)/2*(x/25)` - `5*(x/25)^2`

y = `root()(3)*x` - `x^2/125`

Ezt ábrázoltam a lenti ábrán. Itt látszik, hogy mi a helyzet.

Teljesen igaza van kazahnak, sok megoldás lehet attól függően, hiogy milyen széles az épület és melyik részére esik le a tárgy.
Nincs még megadva valamilyen adat? Mondjuk hogy kocka alakú az épület és éppen a közepére esik le a tárgy?