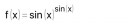Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Bonyolult fuggveny abrazolas
 Attila089
kérdése
Attila089
kérdése
450
Abrazoljuk 0-pi intervallumon a kovetkezo fuggvenyt:
Levezetne valaki lepesenkent,kerem.
Levezetne valaki lepesenkent,kerem.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Az intervallumon a függvény értelmezve van és folytonos.
Először mi a helyzet 0-nál és π-nél?
Ott `0^0` jellegű, úgyhogy határérték kell L'Hopital-lal:
(0-ra írom, de π-nél is ugyanez. A limesz az intervallum belsejéből tart 0-hoz illetve π-hez, szóval végig valós számok vannak.)
`lim_(x -> 0)sinx^(sinx)=lim_(x -> 0) e^(sinx·"ln"sinx)=e^(lim_(x -> 0) sinx·"ln"sinx)`
`lim_(x -> 0) sinx·"ln"sinx=lim_(x -> 0) ("ln"sinx)/(1/sinx)`
Ez már `oo/oo` alakú, lehet H'Hopital-ni:
`d/dx "ln"sinx = 1/sinx·cosx`
`d/dx 1/sinx = -1/sin^2x·cosx`
Ezek hányadosa `-sinx`, aminek a határértéke 0-nál és π-nél is 0.
És mivel `e^0=1`, ezért a `sinx^sinx` függvény értéke az intervallum mindkét szélénél 1.
Aztán mi a helyzet az intervallum közepén? Nézzük a deriváltját, az megadja a menetét valamint a szélsőértékeit:
`d/dx e^(sinx·"ln"sinx) = e^(sinx·"ln"sinx)·(cosx·"ln"sinx+sinx·1/sinx·cosx) =`
`= sinx^sinx·cosx·("ln"sinx+1)`
A tagok zérushelyei:
a) `sinx^sinx` sosem nulla az intervallumon, mindig pozitív
b) `cosx=0` akkor, ha `x=π/2`. Előtte negatív, utána pozitív.
c) `"ln"sinx+1=0` akkor, amikor `sinx=1/e`, vagyis
`x_1="arc"sin(1/e)`
`x_2=π-"arc"sin(1/e)`
A `[0;x_1)` intervallumon `"ln"sinx+1` negatív, aztán pozitív, végül az `(x_2;π]` intervallumon megint negatív.
Vagyis a teljes derivált illetve `f(x)` ilyen:
- A `[0;x_1)` intervallumon negatív a derivált, `f(x)` szigorúan monoton csökken
- `x_1`-nél nulla a derivált, `f(x)`-nek lokális minimuma van
- Az `(x_1;π/2)` intervallumon pozitív a derivált, `f(x)` szigorúan monoton nő
- `π/2`-nél nulla a derivált, `f(x)`-nek lokális maximuma van
- A `(π/2;x_2)` intervallumon negatíva derivált, `f(x)` szigorúan monoton csökken
- `x_2`-nél nulla a derivált, `f(x)`-nek lokális minimuma van
- Az `(x_2;π]` intervallumon pozitív a derivált, `f(x)` szigorúan monoton nő
Még a lokális minimumok és maximum értékét kell kiszámolni, és már egész jól lehet ábrázolni.
---
Lehet, hogy a második deriváltat is ki kell még számolni, ha teljes függvényvizsgálatról van szó; az határozza meg, hogy hol konvex illetve konkáv a függvény. Próbáld meg.
Először mi a helyzet 0-nál és π-nél?
Ott `0^0` jellegű, úgyhogy határérték kell L'Hopital-lal:
(0-ra írom, de π-nél is ugyanez. A limesz az intervallum belsejéből tart 0-hoz illetve π-hez, szóval végig valós számok vannak.)
`lim_(x -> 0)sinx^(sinx)=lim_(x -> 0) e^(sinx·"ln"sinx)=e^(lim_(x -> 0) sinx·"ln"sinx)`
`lim_(x -> 0) sinx·"ln"sinx=lim_(x -> 0) ("ln"sinx)/(1/sinx)`
Ez már `oo/oo` alakú, lehet H'Hopital-ni:
`d/dx "ln"sinx = 1/sinx·cosx`
`d/dx 1/sinx = -1/sin^2x·cosx`
Ezek hányadosa `-sinx`, aminek a határértéke 0-nál és π-nél is 0.
És mivel `e^0=1`, ezért a `sinx^sinx` függvény értéke az intervallum mindkét szélénél 1.
Aztán mi a helyzet az intervallum közepén? Nézzük a deriváltját, az megadja a menetét valamint a szélsőértékeit:
`d/dx e^(sinx·"ln"sinx) = e^(sinx·"ln"sinx)·(cosx·"ln"sinx+sinx·1/sinx·cosx) =`
`= sinx^sinx·cosx·("ln"sinx+1)`
A tagok zérushelyei:
a) `sinx^sinx` sosem nulla az intervallumon, mindig pozitív
b) `cosx=0` akkor, ha `x=π/2`. Előtte negatív, utána pozitív.
c) `"ln"sinx+1=0` akkor, amikor `sinx=1/e`, vagyis
`x_1="arc"sin(1/e)`
`x_2=π-"arc"sin(1/e)`
A `[0;x_1)` intervallumon `"ln"sinx+1` negatív, aztán pozitív, végül az `(x_2;π]` intervallumon megint negatív.
Vagyis a teljes derivált illetve `f(x)` ilyen:
- A `[0;x_1)` intervallumon negatív a derivált, `f(x)` szigorúan monoton csökken
- `x_1`-nél nulla a derivált, `f(x)`-nek lokális minimuma van
- Az `(x_1;π/2)` intervallumon pozitív a derivált, `f(x)` szigorúan monoton nő
- `π/2`-nél nulla a derivált, `f(x)`-nek lokális maximuma van
- A `(π/2;x_2)` intervallumon negatíva derivált, `f(x)` szigorúan monoton csökken
- `x_2`-nél nulla a derivált, `f(x)`-nek lokális minimuma van
- Az `(x_2;π]` intervallumon pozitív a derivált, `f(x)` szigorúan monoton nő
Még a lokális minimumok és maximum értékét kell kiszámolni, és már egész jól lehet ábrázolni.
---
Lehet, hogy a második deriváltat is ki kell még számolni, ha teljes függvényvizsgálatról van szó; az határozza meg, hogy hol konvex illetve konkáv a függvény. Próbáld meg.
0
- Még nem érkezett komment!