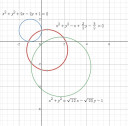Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Koordináta-Geometria
 Napocska
kérdése
Napocska
kérdése
1710
Határozzuk meg a kör közêppontjának koordinátáit és sugarát,ha egyenlete: a.) x^2+y^2-x+ 3/2y - 5/2 = 0 b.) x^2+y^2+2x-2y+1=0. c.) x^2+y^2 = √12 x - √20 y -1
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
A teljes négyzetté alakítás úgy történik, hogy felhasználjuk az `(x-a)^2` = `x^2`-2ax+`a^2` azonosságot.
a, `x^2`+`y^2`-x+ 3/2y - 5/2 = (`x^2`-x+`1/4`)+(`y^2`+`3/2y`+`9/16`)-(`5/2`+`1/4`+`9/16`)=
= `(x-1/2)^2` + `(y+3/4)^2` - `(40+4+9)/16` = 0
`(x-1/2)^2` + `(y+3/4)^2`= `53/16`
A kör középpontjának koordinátái: O(`1/2`;`-3/4`),
A kör sugara: r = `root()(53/16)`
b,
`x^2`+`y^2`+2x-2y+1=0= (`x^2`+2x+1)+(`y^2`+2y+1)+(1-1-1)= `(x+1)^2` + `(y-1)^2`-1=0
A kör egyenlete:
`(x+1)^2` + `(y-1)^2`=1
A kör középpontjának koordinátái: O(`-1`;`-1`),
A kör sugara: r = 1
c,
`root()(12)` = `2*root()(3)`
`root()(20)` = `2*root()(5)`
`x^2`+`y^2` = `root()(12)*x` - `root()(20)*y` -1
`x^2`-`2*root()(3)*x`+`root()(3)^2` + `y^2`+`2*root()(5)*y`+`root()(5)^2` -(3+5-1) = 0
`(x-root()(3))^2`+ `(y-root()(5))^2` = 7 = `root()(7)^2`
A kör középpontjának koordinátái: O(`root()(3)`;`-root()(5)`),
A kör sugara: r = `root()(7)`
a, `x^2`+`y^2`-x+ 3/2y - 5/2 = (`x^2`-x+`1/4`)+(`y^2`+`3/2y`+`9/16`)-(`5/2`+`1/4`+`9/16`)=
= `(x-1/2)^2` + `(y+3/4)^2` - `(40+4+9)/16` = 0
`(x-1/2)^2` + `(y+3/4)^2`= `53/16`
A kör középpontjának koordinátái: O(`1/2`;`-3/4`),
A kör sugara: r = `root()(53/16)`
b,
`x^2`+`y^2`+2x-2y+1=0= (`x^2`+2x+1)+(`y^2`+2y+1)+(1-1-1)= `(x+1)^2` + `(y-1)^2`-1=0
A kör egyenlete:
`(x+1)^2` + `(y-1)^2`=1
A kör középpontjának koordinátái: O(`-1`;`-1`),
A kör sugara: r = 1
c,
`root()(12)` = `2*root()(3)`
`root()(20)` = `2*root()(5)`
`x^2`+`y^2` = `root()(12)*x` - `root()(20)*y` -1
`x^2`-`2*root()(3)*x`+`root()(3)^2` + `y^2`+`2*root()(5)*y`+`root()(5)^2` -(3+5-1) = 0
`(x-root()(3))^2`+ `(y-root()(5))^2` = 7 = `root()(7)^2`
A kör középpontjának koordinátái: O(`root()(3)`;`-root()(5)`),
A kör sugara: r = `root()(7)`
0
- Még nem érkezett komment!