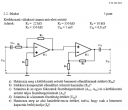
Megoldanátok ezt az elektronikai feladatot.

a)
Ez a kérdés elég hanyagul van megfogalmazva. Nem adták meg, hogy milyen frekvenciájú bemenetről beszélünk, a kapacitív csatolás miatt ugyebár ez számítana. Viszont nem impedanciáról, hanem ellenállásról beszélnek, ebből az következne, hogy a DC-n mérhető bemeneti ellenállásra kíváncsiak. Ez viszont a csatolókondenzátor miatt végtelen. Én azt tartom a legvalószínűbbnek, hogy a kondenzátorral itt nem kell foglalkozni, hanem számoljuk ki a bemeneti ellenállást olyan nagy frekvenciájú jelre, amely mellett a kondenzátort már rövidzárnak lehet tekinteni.

Az ideális műveleti erősítő bemenetébe nem folyik áram, emiatt `R_2` földpotenciálra húzza a neminvertáló bemenetet, ez pedig az invertáló bemenetet is földpotenciálra kényszeríti. Vagyis az egész áramkör a bemenet felől úgy látszik, mintha csak az `R_1` ellenállás lenne ott:

`R_{be}=R_1=22\text{k}Omega`



b)
Az `R_2` kompenzáló ellenállás szerepe az, hogy nem teljesen ideális műveleti erősítő esetén a bemenetekbe befolyó áram miatt fellépő ofszethibát kiküszöböli. Levezethető, hogy az ideális értéke:

`R_2=R_1 times R_3=(R_1R_3)/(R_1+R_3)=20.625\text{k}Omega`



c)
Az első fokozat egy invertáló alapkapcsolás:

`A_{u1}=-R_3/R_1=-15`

A második pedig egy neminvertáló alapkapcsolás:

`A_{u2}=1+R_5/R_4=16`

Az eredő erősítés tehát:

`A_{u}=A_{u1}A_{u2}=-15*16=-240`



d)
`U_{ki}=A_u U_{be}=-240*5\text{mV}=-1.2\text{V}`



e)
Ez olyan, mintha az első fokozat bemeneti ellenállását `R_1`-ről `R_1+1/(j omega C_{be})` impedanciára cserélnénk. Az erősítő átviteli karakterisztikája ekkor:

`A_{u}(j omega)=A_{u1}(j omega) A_{u2}``=``-R_3/(R_1+1/(j omega C_{be}))*16``=``(-16 j omega C_{be} R_3)/(j omega C_{be} R_1+1)`

Ennek az átviteli karakterisztikának a pólusa `1/(R_1 C_{be})`, tehát a határfrekvencia `f_h``=``1/(2 pi R_1 C_{be})``~~``1.06\text{Hz}`.