Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Nagyon fontos lenne, nem sikerül megoldanom
Törölt
kérdése
425
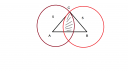
Az ABC háromszög derékszögű, az 5 cm sugarú körök középpontja az átfogó egyik, illetve másik végpontja, és a körök áthaladnak a derékszögű csúcson. Mekkora a vonalkázott rész?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2
horza.2k
megoldása
Mivel a fekete háromszög egyenlő szárú derékszögű háromszög, így Pitagorász szerint a középpontok távolsága `sqrt(5^2+5^2)=sqrt(50)`
Ha a C pontból merőlegest bocsátunk az AB szakaszra, akkor szögfüggvénnyel meghatározhatjuk pl. a B csúcsnál lévő szöget `cos(beta)=(sqrt(50)/2)/5=sqrt(50)/10=sqrt(50/100)=1/sqrt(2)=sqrt(2)/2`
azaz a B csúcsnál lévő szög 45°-os, ami a 360°-nak a nyolcada
Így a 45°-os körcikk területe `(5^2*pi)/8`
ebből kivonjuk a C, lefelé merőleges és B háromszög területét `(sqrt(50)/2)^2/2=(50/4)/2=50/8`
így megkapjuk a metszet negyedét - a keresett terület a metszet fele, tehát a negyedet duplázni kell
`T=2*((5^2*pi)/8-50/8)=((25*pi)-50)/4=(25*(pi-2))/4`
Ha a C pontból merőlegest bocsátunk az AB szakaszra, akkor szögfüggvénnyel meghatározhatjuk pl. a B csúcsnál lévő szöget `cos(beta)=(sqrt(50)/2)/5=sqrt(50)/10=sqrt(50/100)=1/sqrt(2)=sqrt(2)/2`
azaz a B csúcsnál lévő szög 45°-os, ami a 360°-nak a nyolcada
Így a 45°-os körcikk területe `(5^2*pi)/8`
ebből kivonjuk a C, lefelé merőleges és B háromszög területét `(sqrt(50)/2)^2/2=(50/4)/2=50/8`
így megkapjuk a metszet negyedét - a keresett terület a metszet fele, tehát a negyedet duplázni kell
`T=2*((5^2*pi)/8-50/8)=((25*pi)-50)/4=(25*(pi-2))/4`
1
- Még nem érkezett komment!
szzs
{ Fortélyos }
válasza
A kérdezőnek a saját rajzát kellene először is elfelejteni! Itt a jó rajz:
1
- Még nem érkezett komment!