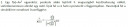Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Mechanika
 makákó
kérdése
makákó
kérdése
534
Sziasztok!
A feladat a csatolt képen található. Ha van akinek van 5lete, és ezt le is vezetné, azt megköszönném. Megérteni szeretném a feladatot, nem pedig csak másolni. Köszönöm a segítséget!
A feladat a csatolt képen található. Ha van akinek van 5lete, és ezt le is vezetné, azt megköszönném. Megérteni szeretném a feladatot, nem pedig csak másolni. Köszönöm a segítséget!
Jelenleg 1 felhasználó nézi ezt a kérdést.
parabola, egyenlet, magasság, kezdősebesség, súrlódás, nyomóerő, erő, függvény, simulókör
parabola, egyenlet, magasság, kezdősebesség, súrlódás, nyomóerő, erő, függvény, simulókör
0
Felsőoktatás / Fizika
Válaszok
2 bongolo
{
bongolo
{  }
válasza
}
válasza
Szerintem így mehet:
Nincs súrlódás, tehát a kezdeti helyzeti energia lesz a pillanatnyi helyzeti és mozgási összege. Ebből a sebesség számolható x függvényében.
Aztán a simulókör sugara azért fontos, mert ki lehet vele számolni az m·v²/r centripetális erőt, és az a kérdés.
A levezetés ugye megy?
Nincs súrlódás, tehát a kezdeti helyzeti energia lesz a pillanatnyi helyzeti és mozgási összege. Ebből a sebesség számolható x függvényében.
Aztán a simulókör sugara azért fontos, mert ki lehet vele számolni az m·v²/r centripetális erőt, és az a kérdés.
A levezetés ugye megy?
0
-
makákó: Az a gond, hogy középsuliban csak egy évig volt fizikám, és most egyetemen ez így hirtelen elég nagy falat, és órán meg nem ilyeneket csinálunk :/ elég sok mindent kell bepótolnom 6 éve 0
 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Az induló helyzeti energia: `E=m·g·h`
`x`-nél a magasság `h_x=Ax^2`.
Ott van helyzeti meg mozgási is:
Helyzeti: `E_(hx)=m·g·h_x=m·g·Ax^2`
Mozgási: `E_(mx)=E-E_(hx)` hisz a kettő összege `E` kell legyen.
A mozgási persze `1/2·m·v^2`:
`1/2·m·v^2 =E_(mx)=m·g·h-m·g·Ax^2`
`v^2 =2g(h-Ax^2)`
Körmozgáskor van centripetális erő, ami merőleges a felületre (hisz a kör középpontja felé mutat). Az kell ahhoz, hogy körpályán tartsa a testet. Ezt még gimiben tanultátok. Amit most tanultatok az meg az, hogy tetszőleges görbe pályán is a pillanatnyi erőnek az a komponense, ami merőleges a felületre (az a nyomóerő egyébként), az is a centripetális erő, ugyanúgy kell számolni, mint körpályánal, csak a sugár a simulókör sugara.
`F_(cp)=m·v^2/r`
`F_(cp)(x)=m·(2g(h-Ax^2))/(R(x))`
Most már csak a deriválásokat kell megcsinálni az `1//R(x)`-hez:
`f(x)=Ax^2`
`(df)/(dx)=2Ax`
`(d^2f)/(dx^2)=2A`
`1/(R(x))=(2A)/(1+(2Ax)^2)^(3/2)`
`F_(cp)(x)=m·2g(h-Ax^2)(2A)/(1+(2Ax)^2)^(3/2)`
`x`-nél a magasság `h_x=Ax^2`.
Ott van helyzeti meg mozgási is:
Helyzeti: `E_(hx)=m·g·h_x=m·g·Ax^2`
Mozgási: `E_(mx)=E-E_(hx)` hisz a kettő összege `E` kell legyen.
A mozgási persze `1/2·m·v^2`:
`1/2·m·v^2 =E_(mx)=m·g·h-m·g·Ax^2`
`v^2 =2g(h-Ax^2)`
Körmozgáskor van centripetális erő, ami merőleges a felületre (hisz a kör középpontja felé mutat). Az kell ahhoz, hogy körpályán tartsa a testet. Ezt még gimiben tanultátok. Amit most tanultatok az meg az, hogy tetszőleges görbe pályán is a pillanatnyi erőnek az a komponense, ami merőleges a felületre (az a nyomóerő egyébként), az is a centripetális erő, ugyanúgy kell számolni, mint körpályánal, csak a sugár a simulókör sugara.
`F_(cp)=m·v^2/r`
`F_(cp)(x)=m·(2g(h-Ax^2))/(R(x))`
Most már csak a deriválásokat kell megcsinálni az `1//R(x)`-hez:
`f(x)=Ax^2`
`(df)/(dx)=2Ax`
`(d^2f)/(dx^2)=2A`
`1/(R(x))=(2A)/(1+(2Ax)^2)^(3/2)`
`F_(cp)(x)=m·2g(h-Ax^2)(2A)/(1+(2Ax)^2)^(3/2)`
1
-
makákó: Köszönöm! 6 éve 0
-
makákó: Át fogom nézni! 6 éve 0