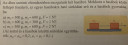Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Fizika Sos dolgozat
 Attila089
kérdése
Attila089
kérdése
487
Holnap dolgozat lesz es a kiosztott peldak lesznek benne amikbol ezekkel nem boldogultam valaki segitsen kerem.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Fizika
Válaszok
4 bongolo
{
bongolo
{  }
megoldása
}
megoldása
105)
Az első szakaszok nő a sebesség, tehát gyorsul a lift. Gondolom felfelé vitték a terhet, úgyhogy felfelé gyorsult. Ilyenkor a kötélnek nem csak tartania kell a 2000 N terhet, hanem még plusz erővel gyorsítania is. A plusz erő `F=m·a`. A gyorsulás abból látszik, hogy 1 másodperc alatt 2 m/s-re nőtt a sebessége, tehát `a_1=(Δv)/(Δt)=(2\ m/s)/(1\ s)=2 m/s^2`
A gyorsító erő tehát `F=200\ kg·2 m/s^2`. Az összes erő, amit a drótkötél kifejt, ennek és a súlynak az összege.
Aztán a középső szakaszon állandó a sebesség, itt nem gyorsul. Ott a gyorsító erő nulla, csak tartja a kötél a terhet 2000 N-nal.
A harmadik szakaszon csökken a sebesség: fél másodperc alatt 0,8 m/s-mal. Itt a gyorsulás `a_3=(Δv)/(Δt)=("-0,8" m/s)/("0,5"\ s)`, negatív (mert csökken a sebesség). Az erő is negatív: `F_3=m·a_3`
Az összes erő most is a súlynak és ennek az `F_3`-nak az összege, de mivel `F_3` negatív, ki lesz vonva 2000-ből.
a) A drótkötélnek ezek közül a legnagyobbat kell kibírnia, az az első szakaszon volt.
b) Az eredő erő az, ami gyorsítja a testet. Tehát ez az `m·a_(123)` erő. Rajzold fel őket. Vízszintes itt is az idő, függőleges meg az erő. Az egyes szakaszokon állandó az erő, tehát vízszintes szakaszok lesznek. A harmadik szakaszon negatív!!!
c) Ezt is kiszámoltad, ez az összes erő: `m·g+m·a_(123)`
Az első szakaszok nő a sebesség, tehát gyorsul a lift. Gondolom felfelé vitték a terhet, úgyhogy felfelé gyorsult. Ilyenkor a kötélnek nem csak tartania kell a 2000 N terhet, hanem még plusz erővel gyorsítania is. A plusz erő `F=m·a`. A gyorsulás abból látszik, hogy 1 másodperc alatt 2 m/s-re nőtt a sebessége, tehát `a_1=(Δv)/(Δt)=(2\ m/s)/(1\ s)=2 m/s^2`
A gyorsító erő tehát `F=200\ kg·2 m/s^2`. Az összes erő, amit a drótkötél kifejt, ennek és a súlynak az összege.
Aztán a középső szakaszon állandó a sebesség, itt nem gyorsul. Ott a gyorsító erő nulla, csak tartja a kötél a terhet 2000 N-nal.
A harmadik szakaszon csökken a sebesség: fél másodperc alatt 0,8 m/s-mal. Itt a gyorsulás `a_3=(Δv)/(Δt)=("-0,8" m/s)/("0,5"\ s)`, negatív (mert csökken a sebesség). Az erő is negatív: `F_3=m·a_3`
Az összes erő most is a súlynak és ennek az `F_3`-nak az összege, de mivel `F_3` negatív, ki lesz vonva 2000-ből.
a) A drótkötélnek ezek közül a legnagyobbat kell kibírnia, az az első szakaszon volt.
b) Az eredő erő az, ami gyorsítja a testet. Tehát ez az `m·a_(123)` erő. Rajzold fel őket. Vízszintes itt is az idő, függőleges meg az erő. Az egyes szakaszokon állandó az erő, tehát vízszintes szakaszok lesznek. A harmadik szakaszon negatív!!!
c) Ezt is kiszámoltad, ez az összes erő: `m·g+m·a_(123)`
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
103)
Ha a csomag tömege `m`, akkor a súlya `m·g`, a maximális surlódása pedig `F_(smax)=µ·m·g`.
(Nem tudjuk a tömeget, csak reménykedhetünk, hogy ki fog esni.)
Ez a surlódás adja azt az erőt, ami gyorsítja a csomagot. A maximálsi gyorsítás az `F=m·a`-ból jön ki:
`F_(smax)=m·a_(max)`
`µ·m·g=m·a_(max)`
`µ·g=a_(max)`
Tényleg kiesett az `m`. Számold ki `a_(max)`-ot. Jó, kiszámoltam én is, `"2,5" m/s^2`
Ha tudja ugyanolyan gyorsítással gyorsítani, mint ahogy az autó gyorsul (tehát ha `a_(auto) ≤ a_(max)`), akkor nem csúszik meg a csomag. (És persze akkor a gyorsító erő is ≤ `F_(smax)`-nál, pont annyi csak, amennyi kell az `a_(auto)` nagyságú gyorsuláshoz.)
Szóval ki kellene számolni, hogy ha éppen a legnagyobb lehetséges `a_(max)` a kocsi gyorsulása, akkor mekkora úton gyorsul fel 15 m/s-ra:
Tudjuk a gyorsuló mozgás útjának a képletét:
`s=1/2·a·t^2`
de most bejött az idő. Az idővel tudunk sebesség-képletet is:
`v=a·t`
`15 m/s="2,5" m/s^2·t`
ebből kijön az idő, azt meg írd be a fenti `s=...` képletbe, meglesz az út.
Ha a csomag tömege `m`, akkor a súlya `m·g`, a maximális surlódása pedig `F_(smax)=µ·m·g`.
(Nem tudjuk a tömeget, csak reménykedhetünk, hogy ki fog esni.)
Ez a surlódás adja azt az erőt, ami gyorsítja a csomagot. A maximálsi gyorsítás az `F=m·a`-ból jön ki:
`F_(smax)=m·a_(max)`
`µ·m·g=m·a_(max)`
`µ·g=a_(max)`
Tényleg kiesett az `m`. Számold ki `a_(max)`-ot. Jó, kiszámoltam én is, `"2,5" m/s^2`
Ha tudja ugyanolyan gyorsítással gyorsítani, mint ahogy az autó gyorsul (tehát ha `a_(auto) ≤ a_(max)`), akkor nem csúszik meg a csomag. (És persze akkor a gyorsító erő is ≤ `F_(smax)`-nál, pont annyi csak, amennyi kell az `a_(auto)` nagyságú gyorsuláshoz.)
Szóval ki kellene számolni, hogy ha éppen a legnagyobb lehetséges `a_(max)` a kocsi gyorsulása, akkor mekkora úton gyorsul fel 15 m/s-ra:
Tudjuk a gyorsuló mozgás útjának a képletét:
`s=1/2·a·t^2`
de most bejött az idő. Az idővel tudunk sebesség-képletet is:
`v=a·t`
`15 m/s="2,5" m/s^2·t`
ebből kijön az idő, azt meg írd be a fenti `s=...` képletbe, meglesz az út.
Módosítva: 6 éve
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
A harmadik ábra, nem látszik a feladat száma.
Az egyes testekre ilyen erők hatnak:
`m_1`-re: `F` húzóerő jobbra, `K` kötélerő balra, `µ_1·m_1·g` surlódás balra. Ennek a háromnak az eredője gyorsítja:
`F-K-µ_1·m_1·g=m_1·a`
`m_2`-re ható erők: `K` kötélerő jobbra, `µ_2·m_2·g` surlódás balra. Ennek a kettőnek az eedője gyorsítja:
`K-µ_2·m_2·g=m_2·a`
A két gyorsulás egyforma kell legyen, egyébként a madzag elszakadna.
A fenti két egyenletből csak az `a` valamint a `K` az ismeretlenek, meg kell oldani mindhárom adatsorra az egyenletrendszert. Fejezd be. (A grammokat váltsd át kg-ba, hogy minden mértékegység "rendes" legyen, akkor lehet velük számolni csak.)
Az egyes testekre ilyen erők hatnak:
`m_1`-re: `F` húzóerő jobbra, `K` kötélerő balra, `µ_1·m_1·g` surlódás balra. Ennek a háromnak az eredője gyorsítja:
`F-K-µ_1·m_1·g=m_1·a`
`m_2`-re ható erők: `K` kötélerő jobbra, `µ_2·m_2·g` surlódás balra. Ennek a kettőnek az eedője gyorsítja:
`K-µ_2·m_2·g=m_2·a`
A két gyorsulás egyforma kell legyen, egyébként a madzag elszakadna.
A fenti két egyenletből csak az `a` valamint a `K` az ismeretlenek, meg kell oldani mindhárom adatsorra az egyenletrendszert. Fejezd be. (A grammokat váltsd át kg-ba, hogy minden mértékegység "rendes" legyen, akkor lehet velük számolni csak.)
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
104)
A tej majd 90%-a víz, ezért a teh fajsúlya nagyon hasonlít a vízére, tehát 6 liter tej az kb. 6 kg. Összesen tehát kábé 8 kg van a szatyorban.
a) Ha áll a lift, akkor ez 80 N.
b) Ha állandó sebességgel megy a lift, az ugyanolyan, mintha állna. A lényeg, hogy a gyorsulás ilyenkor nulla. A súlya ilyenkor is 80 N.
c) He felfelé gyorsul, akkor a kezünk nem csak tartja a szatyrot, hanem még pluszban gyorsítja is, tehát nagyobb erő kell hozzá. `F=m·g+m·a`, számold ki.
d) Ha lefelé gyorsul (esik), akkor nem kell `m·g` erő ahhoz, hogy tartsuk. Pont olyan, mintha negatív lenne a gyorsulása. `F=m·g-m·a`
A tej majd 90%-a víz, ezért a teh fajsúlya nagyon hasonlít a vízére, tehát 6 liter tej az kb. 6 kg. Összesen tehát kábé 8 kg van a szatyorban.
a) Ha áll a lift, akkor ez 80 N.
b) Ha állandó sebességgel megy a lift, az ugyanolyan, mintha állna. A lényeg, hogy a gyorsulás ilyenkor nulla. A súlya ilyenkor is 80 N.
c) He felfelé gyorsul, akkor a kezünk nem csak tartja a szatyrot, hanem még pluszban gyorsítja is, tehát nagyobb erő kell hozzá. `F=m·g+m·a`, számold ki.
d) Ha lefelé gyorsul (esik), akkor nem kell `m·g` erő ahhoz, hogy tartsuk. Pont olyan, mintha negatív lenne a gyorsulása. `F=m·g-m·a`
0
-
Attila089: Nagyon sokat segitett, koszonom szepen 6 éve 0