Diszkrét idejű rendszer

Az első késleltető bemenetére felírható egyenlet:

`zX_1(z)=aU(z)+bY(z)`

A második késleltető bemenete az első késleltető kimenete:

`X_1(z)=zX_2(z)`

A rendszer kimenete pedig:

`Y(z)=X_2(z)+cX_1(z)+U(z)`

Ezek alapján kell kifejeznünk `Y(z)`-t `U(z)`-vel. Fejezzük ki a második egyenletből `X_2(z)`-t és helyettesítsük be a harmadik egyenletbe:

`Y(z)=X_1(z)*(1/z+c)+U(z)`

Most az első egyenletből fejezzük ki `X_1(z)`-t, és helyettesítsük be ebbe:

`Y(z)=(aU(z)+bY(z))/z*(1/z+c)+U(z)=(aU(z)+bY(z))/z^2+(acU(z)+bcY(z))/z+U(z)`

`Y(z)[1-b/z^2-(bc)/z]=U(z)[1+a/z^2+(ac)/z]`

`Y(z)[z^2-bcz-b]=U(z)[z^2+acz+a]`

`H(z)=(Y(z))/(U(z))=(z^2+acz+a)/(z^2-bcz-b)=(z^2-1.8z+0.45)/(z^2+0.32z-0.08)`

A zérusok a számláló, a pólusok a nevező gyökei:
`z_1=1.5`
`z_2=0.3`
`p_1~~-0.4850`
`p_2~~0.1650`

Az impulzusválaszhoz bontsuk fel parciális törtekre az átviteli függvényt:

`H(z)=(z^2-1.8z+0.45)/(z^2+0.32z-0.08)~~1-2.3974/(z + 0.4850) + 0.2774/(z - 0.1650)`

Ennek az inverz z-transzformáltja az impulzusválasz:

`h[k]~~delta[k]-2.3974 epsilon[k-1]*(-0.4850)^(k-1)+0.2774 epsilon[k-1]*(0.1650)^(k-1)`

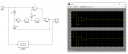
Mellékeltem egy Simulink szimulációt, ami szerint jól számoltam. (Az eredeti hálózatmodell és a kész átviteli függvény ugrásválaszát hasonlítottam össze, jól láthatóan egyeznek.)