Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
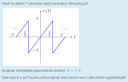
Jel Fourier-polinómjának együtthatói
 Pikarc
kérdése
Pikarc
kérdése
595
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
bme, Rendszerelmélet, fourier-polinom
bme, Rendszerelmélet, fourier-polinom
0
Felsőoktatás / Egyéb
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A Fourier-sornak sokféle alakja van, nem mondtad, hogy melyiket keresed. Én sima valós szinuszos bázisfüggvények terében fogom sorba fejteni a jelet. A jel nulla középértékű páratlan függvény, tehát a Fourier-sornak csak szinuszos tagjai lesznek:
`x(t)=sum_{k=1}^{oo} C_k sin(k (2pi)/T t)`
A keresett együtthatók:
`C_k = 2/T int_{-T/2}^{T/2} x(t) sin(k (2pi)/T t) dt`
Az integrálási határok tetszőlegesen választhatók, csak az a lényeg, hogy pontosan egy egész periódust integráljunk. Én azért fogok a `[-T/2, T/2]` intervallumon integrálni, mert itt a függvény nagyon egyszerűen leírható: `x(t)=(2A)/T t`. Innen az együtthatók:
`C_k = 2/T int_{-T/2}^{T/2} (2A)/T t sin(k (2pi)/T t) dt``=``(4A)/T^2 int_{-T/2}^{T/2} t sin(k (2pi)/T t) dt`
Tehát egy `int t sin (alpha t) dt` alakú integrált kell kiszámítanunk. Ez parciális integrálásért kiált: `int f dg = fg - int g df`, ahol most `f=t` és `dg = sin (alpha t) dt`. Ekkor `df = dx` és `g = -cos(alpha t)/alpha`, tehát az integrál:
`int t sin (alpha t) dt``=``-t cos(alpha t)/alpha + int cos(alpha t)/alpha dt``=``-t cos(alpha t)/alpha + sin(alpha t)/alpha^2 + c`
A mi esetünkben `alpha=k (2pi)/T`:
`C_k=(4A)/T^2[-t cos(k (2pi)/T t)/(k (2pi)/T)+sin(k (2pi)/T t)/(k (2pi)/T)^2]_{-T/2}^{T/2}``=``(4A)/T^2[-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2-T/2 cos(-k pi)/(k (2pi)/T)-sin(-k pi)/(k (2pi)/T)^2]`
A szinusz páratlan és a koszinusz páros voltát kihasználva:
`C_k=(4A)/T^2[-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2]``=``(4A)/T^2[-T cos(k pi)/(k (2pi)/T)+2sin(k pi)/(k (2pi)/T)^2]`
Azt is tudjuk, hogy `cos(k pi)=(-1)^k` és `sin(k pi)=0`:
`C_k=(4A)/T^2[-T (-1)^k/(k (2pi)/T)]=(-1)^(k+1) (4A)/(k 2pi)=(-1)^(k+1) 19.6/(k pi)`
Kiszámítva az első néhány értéket:
`C_1=19.6/pi~~6.239`
`C_2=-19.6/(2pi)~~-3.119`
`C_3=19.6/(3pi)~~2.080`
`C_4=-19.6/(4pi)~~-1.560`
`C_5=19.6/(5pi)~~1.248`
Így a jel Fourier-polinomos közelítése az alábbi (T=1 esetére):
`x(t)~~ 6.239sin(2pit)-3.119sin(4pit)+2.080sin(6pit)-1.560sin(8pit)+1.248sin(10pit)`
Ellenőrzés:
https://www.wolframalpha.com/input/?i=6.239*sin(2*pi*t)-3.119*sin(4*pi*t)%2B2.080*sin(6*pi*t)-1.560*sin(8*pi*t)%2B1.248*sin(10*pi*t)
Látható, hogy a Gibbs-oszcillációtól eltekintve már az ötödrendű közelítés is kezd hasonlítani az eredeti jelre.
`x(t)=sum_{k=1}^{oo} C_k sin(k (2pi)/T t)`
A keresett együtthatók:
`C_k = 2/T int_{-T/2}^{T/2} x(t) sin(k (2pi)/T t) dt`
Az integrálási határok tetszőlegesen választhatók, csak az a lényeg, hogy pontosan egy egész periódust integráljunk. Én azért fogok a `[-T/2, T/2]` intervallumon integrálni, mert itt a függvény nagyon egyszerűen leírható: `x(t)=(2A)/T t`. Innen az együtthatók:
`C_k = 2/T int_{-T/2}^{T/2} (2A)/T t sin(k (2pi)/T t) dt``=``(4A)/T^2 int_{-T/2}^{T/2} t sin(k (2pi)/T t) dt`
Tehát egy `int t sin (alpha t) dt` alakú integrált kell kiszámítanunk. Ez parciális integrálásért kiált: `int f dg = fg - int g df`, ahol most `f=t` és `dg = sin (alpha t) dt`. Ekkor `df = dx` és `g = -cos(alpha t)/alpha`, tehát az integrál:
`int t sin (alpha t) dt``=``-t cos(alpha t)/alpha + int cos(alpha t)/alpha dt``=``-t cos(alpha t)/alpha + sin(alpha t)/alpha^2 + c`
A mi esetünkben `alpha=k (2pi)/T`:
`C_k=(4A)/T^2[-t cos(k (2pi)/T t)/(k (2pi)/T)+sin(k (2pi)/T t)/(k (2pi)/T)^2]_{-T/2}^{T/2}``=``(4A)/T^2[-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2-T/2 cos(-k pi)/(k (2pi)/T)-sin(-k pi)/(k (2pi)/T)^2]`
A szinusz páratlan és a koszinusz páros voltát kihasználva:
`C_k=(4A)/T^2[-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2-T/2 cos(k pi)/(k (2pi)/T)+sin(k pi)/(k (2pi)/T)^2]``=``(4A)/T^2[-T cos(k pi)/(k (2pi)/T)+2sin(k pi)/(k (2pi)/T)^2]`
Azt is tudjuk, hogy `cos(k pi)=(-1)^k` és `sin(k pi)=0`:
`C_k=(4A)/T^2[-T (-1)^k/(k (2pi)/T)]=(-1)^(k+1) (4A)/(k 2pi)=(-1)^(k+1) 19.6/(k pi)`
Kiszámítva az első néhány értéket:
`C_1=19.6/pi~~6.239`
`C_2=-19.6/(2pi)~~-3.119`
`C_3=19.6/(3pi)~~2.080`
`C_4=-19.6/(4pi)~~-1.560`
`C_5=19.6/(5pi)~~1.248`
Így a jel Fourier-polinomos közelítése az alábbi (T=1 esetére):
`x(t)~~ 6.239sin(2pit)-3.119sin(4pit)+2.080sin(6pit)-1.560sin(8pit)+1.248sin(10pit)`
Ellenőrzés:
https://www.wolframalpha.com/input/?i=6.239*sin(2*pi*t)-3.119*sin(4*pi*t)%2B2.080*sin(6*pi*t)-1.560*sin(8*pi*t)%2B1.248*sin(10*pi*t)
Látható, hogy a Gibbs-oszcillációtól eltekintve már az ötödrendű közelítés is kezd hasonlítani az eredeti jelre.
Módosítva: 6 éve
2
- Még nem érkezett komment!