Biztos volt róla szó, hogy az ötszög átlójának (`d`) és oldalának (`a`) az aránya éppen az aranymetszés:
`d/a=φ=(1+sqrt5)/2`

A csillag oldalait az átlók adják. A csillag belsejében az átlók által egy kis ötszög van kimetszve, aminek az oldala `x`. Számoljuk ki.
Az átló 3 részre van vágva: középen van az `x`, két oldalt meg ami a csillag "kilógó" részének az oldalhossza, nevezzük `b`-nek:
`d=b+x+b`
`b=(d-x)/2`

Az átló párhuzamos a szemben lévő ötszög-oldallal, ezek tehát párhuzamos szelői két másik átlónak (ugye lerajzoltad és látod, miről beszélek?), fel lehet írni a párhuzamos szelők tételével:
`b/x=d/a=φ`
`((d-x)/2)/x=φ`
`d-x=2φx`
`d=(2φ+1)x`
`aφ=(2φ+1)x`
`x=a φ/(2φ+1)=a·((1+sqrt5)/2)/(2·(1+sqrt5)/2+1)=a·((1+sqrt5)/2)/(2+sqrt5)=a·(1+sqrt5)/(4+2sqrt5)`
`x=a·((1+sqrt5)(4-2sqrt5))/(4^2-(2sqrt5)^2)=a·(4+4sqrt5-2sqrt5-2·5)/(-4)=a·(-6+2sqrt5)/(-4)`
`x=a·(3-sqrt5)/2`

Aztán:
`b=x·φ=a·(3-sqrt5)/2·(1+sqrt5)/2=a·(3-sqrt5+3sqrt5-5)/4=a(sqrt5-1)/2`
(Egyébként ez éppen `a/φ`. Nem fontos, csak érdekesség.)

Ezekből már ki tudod számolni a területet gondolom.

Másfajta megoldás: (vannak azért benne közös gondolatok az elsővel)

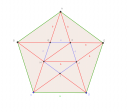
Nézd a mellékelt képet.
- Minden zöld vonal `a=12` hosszúságú
- Minden piros vonal `b`
- Minden kék vonal `c`

`CD` párhuzamos `BE`-vel valamint `HJ`-vel is. Ez azért van, mert a szabályos ötszög tengelyesen szimmetrikus a `CD` oldalfelező merőlegesére.

`CA=CH+HG+GA=b+c+b`

A `CAD` szögben fel lehet írni a párhuzamos szelők tételét:
(Ebből ki fog jönni az aranymetszés, amit az első válaszban feltételeztem, hogy tanultatok)
`(HJ)/(HA)=(GF)/(GA)`
betűkkel:
`b/(b+c)=c/b`
... ami pont az aranymetszés képlete! Ez könnyen kijön:
`(b+c)/b=b/c`
`1+c/b=b/c`
Legyen `x=b/c`
`1+1/x=x`
`x+1=x^2`
`x^2-x-1=0`
Aminek a megoldása:
`x=(1+-sqrt(1^2-4·1·(-1)))/2`
`x=(1+-sqrt5)/2`
Ebből a kettőből csak a pluszos lehet jó, mert a mínuszos negatív szám, és a `b/c` arány nem lehet negatív:
`x=b/c=(1+sqrt5)/2` ami pont az aranymetszés `φ`-vel jelölt értéke.

Most nézzük a területeket:
Az `EFHJ` négyszög egy paralelogramma, hisz `HJ` párhuzamos `FE`-vel, és `HF` is párhuzamos `JE`-vel. Ráadásul mivel `FE=JE=b`, ez rombusz, hisz mind a négy oldala `b`.

A csillag "kilógó" csúcsainak (mint pl. az `FJE` háromszög) területe egyforma, és pont annyi az `FJH` háromszög területe is. Legyen ez a terület `T`. Ez a közepes területű háromszög.
Kellene még tudni a kis `FHG` valamint a nagy `FAE` háromszögek területét, akkor már mindent tudnánk, mert minden más háromszög is ezek valamelyikével egyenlő. Nevezzük ezeket `T_"kis"` és `T_"nagy"` területeknek, vagy röviden `T_k` és `T_n`-nek.

A "kis" háromszög (`FGH`) `T_k` területe:
Nézd az `FG=c` valamint `GB=b` szakaszokat az `FBH` háromszögben. A háromszög `H`-ba futó magassága legyen mondjuk `m`. Ez a közös magassága a "közepes" `GBH` valamin "kis" `FGH` háromszögeknek is. Mivel az alapok aránya az aranymetszés (`b/c=φ`), ezért a területek aránya is aranymetsés:
`T/T_k=φ`

A "nagy" háromszög (`FAE`) `T_n` területe:
Most a `JAE` háromszögben kell nézni a `JF` valamint `FA` alapokat, tehát a `JFE` és `FAE` háromszögeket, amik területe `T` és `T_n`. Azok az alapok is `c` meg `b` hosszúak, tehát a területeik aránya is aranymetszés:
`b/c=T_n/T=φ`

Összesen van 5 darab `T_n`, 6 darab `T` és 2 darab `T_k` háromszög. Tehát az össz-terület:
`5T·φ+6T+2T/φ=T·(5φ+6+2/φ)`
A csillag területe pedig:
`6T+2T/φ=T·(6+2/φ)`

A csillag területének aránya a teljes ötszöghöz képest:
`(6+2/φ)/(5φ+6+2/φ)`

Már csak be kell helyettesíteni a `φ` értékét. Érdemes tudni (bár gyorsan kijön ha nem tudjuk fejből), hogy `1/φ` értéke is könnyű:
`φ=(sqrt5+1)/2`
`1/φ=φ-1=(sqrt5-1)/2`

A terület aránya tehát:
`(6+2/φ)/(5φ+6+2/φ)=(5+sqrt5-1)/((5sqrt5+5)/2+6+sqrt5-1)=2/3·(4+sqrt5)/(5+sqrt5)`
Ezt szorozd be a nagy ötszög területével.