A gyorsítás:
Az elektromos tér munkája (`q·U`) gyorsítja fel az `m` tömegű töltést `v` sebességre:
`q·U=1/2·m·v^2`
`v=sqrt(2U·q/m)`
Ez a mozgó töltés jut be a mágneses mezőbe. Mivel az a sebességre merőleges, ekkora erő hat a töltésekre mindaddig, amíg a mezőben mozognak:
`F=q·v·B`
Ez az erő elmozdítja a töltést, de a sebessége továbbra is merőleges lesz a mágneses indukcióvonalakra, mert abban a síkban hat az erő, ami merőleges a mágneses térre (jobbkézszabály). Vagyis az erő mindig merőleges a sebességre, ez pedig azt jelenti, hogy körpályán fordul el a töltés. Az erő ennek a körmozgásnak a centripetális ereje:
`F_(cp)=m·v^2/r=F=q·v·B`
`v=r·q/m·B`
`sqrt(2U·q/m)=r·q/m·B`
`sqrt(2U)=r·sqrt(q/m)·B`

Ha kicsi lenne ez a sugár, akkor a töltés nem is repülne ki a mágneses térből, hanem azon belül körözne. Viszont bizonyára a sugár sokkal nagyobb annál, mint amilyen vastag a mágneses tér (ami `2·R` vagyis 10 cm vastag), ezért egy körívet megy csak azon belül a töltés, utána kirepül belőle és már egyenes vonalban megy tovább.

A mágneses tér közepétől (tengelyétől) `d=20` centire, vagyis a túlsó végétől `d-R=15` centire van az ernyő. Nagyjából ilyen szögben (`α`) térült el a részecske-sugár:
`"tg"\ α=x/(d-R)`
(Ehhez rajzold fel az ernyőt, rajta az `x` elmozdulást, meg a sugár eredeti illetve elmozdított útját. Az adja azt a háromszöget, amiben a tangenst fel lehet írni.)

Ez nem pontos számolás, hisz a 10 centis mágneses terület elég nagy a 15 centis távolsághoz képest, szóval nem `x`-nek kellene lennie a számlálóban. Mi lenne a pontos szám?:
Ha összesen `α` szöget fordul el a sugár, akkor a kis `r` sugarú körpályán való mozgás során ennyivel kerül odébb a mozgó töltés:
(ehhez rajzolni kell egy `r` sugarú körcikket, a cikk "végéből" megy tovább a sugár egyenes vonalban az ernyőhöz)
- Az `r` sugarú kör középpontjához képes `r` távolságra lép be a töltés a mágneses térbe
- Ahol kilép, ott `r·sin\ α=2R`
- ... és `r·cos\ α` távolságra van, vagyis `r-r·cos\ α=r(1-cos\ α)` távolsággal került odébb.

Szóval valójában ezt kellene felírni az ernyő távolsága és a becsapódás helyével:
`"tg"\ α=(x-r(1-cos\ α))/(d-R)`
Ez jól elbonyolítaná a számolást...

Kicsit pontosabb, de még mindig közelítő számolás az, ha a tengelytől való ernyő-távolságot használjuk a tangensnél:
`"tg"\ α=x/d`
Így megfeleztük a hibát... Számoljunk így közelítően.

`"tg"\ α="10,6"/20`
`α=27,9°`

A mágneses mező vastagságával az előbb már felírtuk ezt:
`r·sin\ α=2R`
`r=(2R)/(sin\ α)=10/"0,468"="21,35"\ cm`

A sugárral meg ez volt felírva:
`sqrt(2U)=r·sqrt(q/m)·B`
Vigyázat! Most már a centiméterről át kell váltani méterbe:
`sqrt(2000)="0,2135"·sqrt(q/m)·"5,3"·10^(-4)`
`sqrt(q/m)=sqrt(2000)/("0,2135"·"5,3"·10^(-4))="3,95"·10^5`
`q/m=1,56·10^(11)`

Hmm, nem jött ki pontosan...
Az eltérés nem róható fel a közelítésnek, lehet, hogy nem jól gondolkodtam...

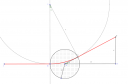
Majdnem jó volt... Most nem fejből csináltam, hanem lerajzoltam, abból már jobban látszik, hogy mi a megoldás.

A rajzon ez látszik:
Az `A` potból indulnak a részecskék, amiket a `B` pont környékén lévő elektródok feszültsége gyorsít fel. A `B` pontnál lépnek be a részecskék a kör keresztmetszerű mágneses térbe. Az indukció-vonalak merőlegesen mennek be a a rajz síkjába a kör alakú területen (a pontok azokat a helyeket szemléltetik, ahol átszúrják a rajz síkját). A részecske-nyaláb körpálya mentén elfordul `α` szöggel, majd a `C` pontban lép ki a mágneses mezőből. Utána egyenes vonalban repül tovább és a `D` pontban éri el az ernyőt. Ha nem lenne bekapcsolva a mágneses mező, akkor az `E` pontban érné el az ernyőt. Ennek a kettőnek a távolsága az `x`.
A kör alakú mégneses mező sugara `R`, a középpont és az ernyő távolsága `d`.
A körpálya középpontja fent van, sugara `r`, a körcikk szöge `α`, és pont ennyi az a szög is, amennyit elfordul a nyaláb..

Az eleje még teljesen jó volt:

A gyorsítófeszültség hatására a végsebesség a munkavégzésből:
`q·U=1/2·m·v^2`
`v=sqrt(2U·q/m)`

A mágneses mezőben a részecskékre ható erő:
`F=q·v·B`
ami éppen a körmozgás centripetális ereje, `F_(cp)=m·v^2/r`
Ebből a kettőből:
`q·v·B=m·v^2/r`
`(q·B)·r/m=v`

Ebbe behelyettesítve az első képlet sebességét:
`(q·B)·r/m=sqrt(2U·q/m)`
`r·sqrt(q/m)·B=sqrt(2U)`

Az első válaszban is ez jött ki ugyanezzel a gondolatmenettel, eddig jó. (Ott kicsit többet magyaráztam...)

Ahol viszont a tangens alfát elkezdtem fejtegetni, az teljesen rossz. Az ábrából látszik, hogy sokkal egyszerűbb a megoldás. Pontosan az egyébként, mint amit én az első válaszban közelítésnek írtam a végén:
`"tg"\ α=x/d="10,6"/20`
`α="27,92"°`

Az `r` sugárra ezt írhatjuk fel: Kösd össze a nagy kör `K` középpontját az `R` sugarú mágneses mező körének `O` középpontjával, ez felezi alfát. A `KBO` derékszögű háromszögre ez írható fel:
`R/r="tg" α/2`
`r=R/("tg" α/2)=(5\ cm)/"0,2486"="20,11"\ cm`

A befejezés már ugyanaz, mint az első válaszban (de most kicsit máshogy lett véletlenül felírva, nem baj) : Az elején kiszámoltuk, hogy
`r·sqrt(q/m)·B=sqrt(2U)`
`sqrt(q/m)=sqrt(2U)/(r·B)=sqrt(2000)/("0,2011"·"5,3"·10^(-4))="4,196·10^5`
`q/m="1,76"·10^(11)`

A mértékegséget nem írtam közben, de figyeltem, hogy méterbe legyen átváltva a cm, ezért `C/(kg)` lett.