Gondolom, a gyorsítás pillanatszerű, tehát vehető úgy, hogy van egy pillanat, amikor a sebessége már `1.08v_0`, a távolsága viszont még `r_0`. Ekkor felírhatjuk az energia és a perdület megmaradását a gyorsítás utáni pillanat, valamint az apogeum között:

`1/2m(1.08v_0)^2-(gamma mM)/r_0=1/2mv_{ag}^2-(gamma mM)/r_{ag}`

`m*1.08v_0*r_0=m v_{ag} r_{ag}`

Egyszerűsítve az űrhajó tömegével:

`1/2(1.08v_0)^2-(gamma M)/r_0=1/2v_{ag}^2-(gamma M)/r_{ag}`

`1.08v_0 r_0=v_{ag} r_{ag}`

A második egyenletből fejezzük ki a földtávolbeli sebességet (`v_{ag}=(1.08v_0 r_0)/r_{ag}`) és helyettesítsük be az első egyenletbe:

`1/2(1.08v_0)^2-(gamma M)/r_0=1/2((1.08v_0 r_0)/r_{ag})^2-(gamma M)/r_{ag}`

`1.08^2/2 v_0^2-(gamma M)/r_0=1.08^2/2(v_0^2 r_0^2)/r_{ag}^2-(gamma M)/r_{ag}`

Azt is tudjuk, hogy a gyorsítás előtt körmozgást végzett, tehát a gravitációs erő szolgáltatta a centripetális erőt:

`(gamma m M)/r_0^2=(m v_0^2)/r_0`

Innen:

`v_0^2=(gamma M)/r_0`

Helyettesítsük be ezt is:

`1.08^2/2 (gamma M)/r_0-(gamma M)/r_0=1.08^2/2(gamma M r_0)/r_{ag}^2-(gamma M)/r_{ag}`

`1.08^2/2 1/r_0-1/r_0=1.08^2/2 r_0/r_{ag}^2-1/r_{ag}`

`1.08^2/2 -1=1.08^2/2 r_0^2/r_{ag}^2-r_0/r_{ag}`

`1.08^2/2 r_0^2/r_{ag}^2-r_0/r_{ag}+1-1.08^2/2 =0`

Másodfokú egyenletet kaptunk a távolságok arányára. Az `r_0=r_{ag}` eseten kívüli megoldás a megoldóképlet alapján:

`r_0/r_{ag}~~0.7147`

Vagyis `r_{ag}~~1.4r_0`, azaz az új földtávolpont kb. 40%-kal messzebb van az eredeti sugárnál.




Ami a pálya egyenletét illeti, itt van levezetve a lap alján, hogy mit kell csinálni:
http://arpad.elte.hu/~bene/elmfiz1/03/3b_eloadas.html

Eszerint az alábbi differenciálegyenletet kell megoldani:

`(d^2 xi)/(d varphi^2)+xi=(gamma M m^2)/(1.08 m v_0 r_0)^2`

ahol `xi=1/r`. Egyszerűsítsünk a tömeggel és használjuk ki megint, hogy `v_0^2=(gamma M)/r_0`:

`(d^2 xi)/(d varphi^2)+xi=1/(1.08^2 r_0)`

A megoldást keressük `xi(varphi)=A+Bcos varphi` alakban! Ekkor a diffegyenlet:

`xi''+xi=1/(1.08^2 r_0)`

`-B cos varphi+A+Bcos varphi=1/(1.08^2 r_0)`

Innen `A=1/(1.08^2 r_0)`. Ezen kívül annak a feltételnek is teljesülnie kell, hogy a kezdeti távolság `r_0`, tehát `xi(0)=1/r_0`:

`1/(1.08^2 r_0)+B cos 0 = 1/r_0`

`1/(1.08^2 r_0)+B = 1/r_0`

`B = 1/r_0 (1-1/(1.08^2))`

Tehát a megoldás:

`xi(varphi)=1/(1.08^2 r_0)+1/r_0 (1-1/(1.08^2)) cos varphi``=``(1/1.08^2+(1-1/1.08^2)cos varphi)/r_0``~~``(0.8573+0.1427cos varphi)/r_0`

Innen a pálya egyenlete:

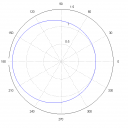
`r(varphi)=1/(xi(varphi))~~r_0/(0.8573+0.1427cos varphi)`

A pálya tehát ellipszis, mellékeltem róla képet is `r_0=1` esetére.