Keresés


Toplista

Toplista
  • betöltés...

Magántanár kereső

Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!

Hogyan történik az alábbi egyszerűsítés az alábbi komplex számnál?

279
(gyök(2))^17 * e^(2 * (8/4)pi + 1/4pi)i = (gyök(2))^17 * e^(pi/4)i

Igazából az "éados" kifejezés nem egyértelmű. Hogyan lehet így leegyszerűsíteni ,hogy az jöjjön ki, mint ami az egyenlőség után van.

A válaszokat előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika

Válaszok

1
A szám szöge `2*8/4 pi + pi/4=4pi+pi/4`. Az `e^(varphi i)` függvény `2 pi` szerint periodikus, tehát `e^((varphi+k*2pi) i)=e^(varphi i)`.

`(sqrt(2))^17 e^((4pi + pi/4)i) = (sqrt(2))^17 * e^(pi/4 i) `


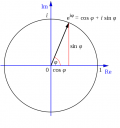
Ennek szemléletes magyarázata az, hogy az `r*e^(varphi i)` szám a komplex síkon az origótól `r` távolságra helyezkedik el és a valós tengelyhez képest `varphi` szögben látszik. Tehát ahogy `varphi` növekszik 0-tól `2pi`-ig, úgy ez a komplex szám egy `r` sugarú körön megy végig. Vagyis ha egy komplex szám szögét `2pi` egész számú többszörösével növeled, akkor visszakapod az eredeti számot, hiszen ez a művelet a komplex számsíkon teljes körbefordulásokat jelent.
Válasz kép
0