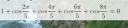Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek feladat
 Törölt
{ Kérdező } kérdése
Törölt
{ Kérdező } kérdése
575
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 szzs
{ Fortélyos }
megoldása
szzs
{ Fortélyos }
megoldása
Egy korábbi feladat jutott eszembe:
https://www.geogebra.org/m/ZQksas6q
Ez alapján folytattam: cos 72°=sin 18°
https://www.geogebra.org/m/ZQksas6q
Ez alapján folytattam: cos 72°=sin 18°
Módosítva: 6 éve
1
-
Törölt: Köszönöm szépen. 6 éve 0
 AlBundy
{ Polihisztor }
válasza
AlBundy
{ Polihisztor }
válasza
A nagyon szép geometriai bizonyítás mellé mutatok egy tisztán algebrait is.
Legyen `S=cos((2pi)/5)+cos((4pi)/5)+cos((6pi)/5)+cos((8pi)/5)`.
`(2pi)/5` és `(8pi)/5` összesen 360°-ot tesznek ki, tehát koszinuszuk ugyanannyi. Ugyanez elmondható a `(4pi)/5` és `(6pi)/5` szögekről is. Ezt kihasználva az összeg két tagjától megszabadulhatunk:
`S=2[cos((2pi)/5)+cos((4pi)/5)]`
Szorozzuk be mindkét oldalt `sin((2pi)/5)`-tel:
`sin((2pi)/5)*S=2[sin((2pi)/5)cos((2pi)/5)+sin((2pi)/5)cos((4pi)/5)]`
Használjuk ki a `sin alpha cos beta=(sin(alpha-beta)+sin(alpha+beta))/2` azonosságot:
`sin((2pi)/5)*S=sin(0)+sin((4pi)/5)-sin((2pi)/5)+sin((6pi)/5)`
`sin(0)=0`, a `(4pi)/5` és `(6pi)/5` szögek összege pedig 360°, tehát szinuszaik egymás ellentettjei, így kiejtik egymást:
`sin((2pi)/5)*S=-sin((2pi)/5)`
Végül osszuk el mindkét oldalt `sin((2pi)/5)`-tel (ami biztosan nem nulla):
`S=-1`
Ebből pedig a bizonyítandó állítás triviálisan következik.
Megjegyzem, hogy ha esetleg tanultál már komplex számokról, akkor a bizonyítás nagyon egyszerű. Ha kihasználod, hogy `cos alpha = (e^(i alpha)+e^(-i alpha))/2`, akkor a bizonyítandó állítás `1+x+x^-1+x^2+x^-2=0` alakban írható, ahol `x=e^(i (2pi)/5)`. Az állítást kicsit átrendezve: `x^-2(1+x+x^2+x^3+x^4)``=``x^-2(x^5-1)/(x-1)=0`, ez pedig teljesül, ha `x ne 1` és `x^5=1`, ami most igaz is.
Legyen `S=cos((2pi)/5)+cos((4pi)/5)+cos((6pi)/5)+cos((8pi)/5)`.
`(2pi)/5` és `(8pi)/5` összesen 360°-ot tesznek ki, tehát koszinuszuk ugyanannyi. Ugyanez elmondható a `(4pi)/5` és `(6pi)/5` szögekről is. Ezt kihasználva az összeg két tagjától megszabadulhatunk:
`S=2[cos((2pi)/5)+cos((4pi)/5)]`
Szorozzuk be mindkét oldalt `sin((2pi)/5)`-tel:
`sin((2pi)/5)*S=2[sin((2pi)/5)cos((2pi)/5)+sin((2pi)/5)cos((4pi)/5)]`
Használjuk ki a `sin alpha cos beta=(sin(alpha-beta)+sin(alpha+beta))/2` azonosságot:
`sin((2pi)/5)*S=sin(0)+sin((4pi)/5)-sin((2pi)/5)+sin((6pi)/5)`
`sin(0)=0`, a `(4pi)/5` és `(6pi)/5` szögek összege pedig 360°, tehát szinuszaik egymás ellentettjei, így kiejtik egymást:
`sin((2pi)/5)*S=-sin((2pi)/5)`
Végül osszuk el mindkét oldalt `sin((2pi)/5)`-tel (ami biztosan nem nulla):
`S=-1`
Ebből pedig a bizonyítandó állítás triviálisan következik.
Megjegyzem, hogy ha esetleg tanultál már komplex számokról, akkor a bizonyítás nagyon egyszerű. Ha kihasználod, hogy `cos alpha = (e^(i alpha)+e^(-i alpha))/2`, akkor a bizonyítandó állítás `1+x+x^-1+x^2+x^-2=0` alakban írható, ahol `x=e^(i (2pi)/5)`. Az állítást kicsit átrendezve: `x^-2(1+x+x^2+x^3+x^4)``=``x^-2(x^5-1)/(x-1)=0`, ez pedig teljesül, ha `x ne 1` és `x^5=1`, ami most igaz is.
Módosítva: 6 éve
1
-
Törölt: Köszönöm nagyon szépen 6 éve 0