Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sebesség vektok, légyszí valaki segítsen megoldani
 Zsuzska
kérdése
Zsuzska
kérdése
489
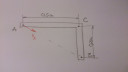
Adott ABC pontok, az " A" pont sebessége vA = 10 m/s. A "B" pont hatásvonala egybeesik a BC egyenessel .Határozza meg a " C" pont sebességvektorát!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Fizika
Válaszok
3 bongolo
{
bongolo
{  }
válasza
}
válasza
Sanos nem igazán értem a feladatot. Hatásvonala valamilyen erőnek szokott lenni, nem pedig pontnak. Ez volt a teljes szövege a feladatnak?
Jó lenne, ha tudnál adni linket a jegyzetedre, amiből tanultok, hogy lássam, mikről van szó.
Jó lenne, ha tudnál adni linket a jegyzetedre, amiből tanultok, hogy lássam, mikről van szó.
0
-
Zsuzska: Íme a teljes feladat: Egy merev rúd B pontjának sebessége vB=10 m/s, a C pont sebességének hatásvonala egybeesik az AC egyenessel. Mekkora az A pont sebességvektora? 6 éve 0
-
bongolo: És milyen irányú a B pont sebessége? (Egyébként eredetileg egy teljesen más feladatot írtál.) 6 éve 0
-
bongolo: Valószínű ehhez a feladathoz, amit most írtál, egy másik ábra tartozik. 6 éve 0
-
Zsuzska: Emlékezetből , írtam, mások segítségét kértem, az ábra jó.A B pont iránya a C pontba mutat. Köszönöm a segítséget előre is. 6 éve 0
-
bongolo: (Nem azért, de nincs sok kedve belegondolni az embernek, ha a kérdező annyi fáradságot nem vesz, hogy elolvassa a saját maga kérdését és az után korrigáljon. Most is fennakadhatnék azon, hogy "a B pont iránya"... egy pontnak nincs iránya, de tudom, mire gondolsz. De azért elkeserítő...) 6 éve 0
 bongolo
{
bongolo
{  }
válasza
}
válasza
A merev test pontjai egyrészt haladó mozgást végeznek, másrészt forgómozgást is. Bizonyára a felrajzolt síkban mozog a test, ami azt jelenti, hogy a forgómozgás szögsebesség vektora merőleges a síkra. Monduk legyen az `x` tengely vízszintes jobbra, az `y` tengely függőleges felfelé, akkor a `z` tengely felénk jön ki a síkból (jobbkézszabály szerint).
Tudjuk elméletből, hogy ha tudjuk az `A` pont sebességét és a test szögsebességét, akkor egy tetszőleges `P` pont sebessége így határozható meg:
`vec(v_P)=vec(v_A)+vec(ω)×vec(r_(AP))`
ahol `vec(ω)` a szögsebesség vektor, `vec(r_(AP))` pedig az `A`-ból `P`-be mutató vektor.
Most pl. `vec(r_(AB))="0,5"·vec(e_x)-"0,3"·vec(e_y)`
Nem tudjuk a szögsebességet, de ez a terv: A `B` pont sebességének tudjuk az irányát, ennek segítségével a fenti képlettel megállapítjuk a szögsebeség nagyságát, utána már a `C` pont sebességét ki tudjuk számolni ugyancsak a fenti képlettel.
Azt tudjuk, hogy a `vec(v_B)` sebességvektor a `B`-ből `C`-be mutató irányban van, vagyis `y` tengely irányú. Ha a hosszát (amit nem ismerünk) `b`-nek nevezzük, akkor:
`vec(v_B)=b·vec(e_y)`
`v_A=10 m/s` a rajz szerinti irányban, írjuk ezt is fel az `x` és `y` irányú egységvektorok segítségével: (a Pitagorasz tétel kell hozzá, meg hogy hasonló háromszögek)
Az `AB` távolság `sqrt("0,5"^2+"0,3"^2)=sqrt(34)/10`
`v_(Ax)=v_A·"0,5"/(sqrt(34)//10)=v_A·5/sqrt(34)=50/sqrt(34)` (nem írom ki a mértékegységeket, de `m/s`)
`v_(Ay)=...=30/sqrt(34)`
Vagyis `vec(v_A)=50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y)`
A `B` pont sebessége:
`vec(v_B)=vec(v_A)+vec(ω)×vec(r_(AB))`
Az `vec(ω)` és az `vec(r_(AB))` vektoriális szorzata merőleges lesz mindkettőre. Vagyis az is a síkban lesz, de merőleges `vec(r_(AB))`-ra. Rajzolj az ábrára a `B` pontban egy merőleges egyenest szaggatottan, ami az `AB` szaggatott egyenesre merőleges. ebben az egyenesben lesz tehát a vektoriális szorzat vektora valahol (vagy fölfelé, vagy lefelé).
`vec(v_B)`-nek csak `vec(e_y)` komponense van, `vec(v_A)`-nak viszont van `vec(e_x)` komponense is. Ez azt jelenti, hogy a vektoriális szorzat `vec(e_x)` komponense ki kell hogy ejtse `vec(v_A)` vízszintes komponensét! Ez a kulcs a megoldáshoz.
... Bocs, majd folytatom, most nem érek rá pillanatnyilag. Addig is gondolkozz rajta, hogy hogyan is tovább.
Tudjuk elméletből, hogy ha tudjuk az `A` pont sebességét és a test szögsebességét, akkor egy tetszőleges `P` pont sebessége így határozható meg:
`vec(v_P)=vec(v_A)+vec(ω)×vec(r_(AP))`
ahol `vec(ω)` a szögsebesség vektor, `vec(r_(AP))` pedig az `A`-ból `P`-be mutató vektor.
Most pl. `vec(r_(AB))="0,5"·vec(e_x)-"0,3"·vec(e_y)`
Nem tudjuk a szögsebességet, de ez a terv: A `B` pont sebességének tudjuk az irányát, ennek segítségével a fenti képlettel megállapítjuk a szögsebeség nagyságát, utána már a `C` pont sebességét ki tudjuk számolni ugyancsak a fenti képlettel.
Azt tudjuk, hogy a `vec(v_B)` sebességvektor a `B`-ből `C`-be mutató irányban van, vagyis `y` tengely irányú. Ha a hosszát (amit nem ismerünk) `b`-nek nevezzük, akkor:
`vec(v_B)=b·vec(e_y)`
`v_A=10 m/s` a rajz szerinti irányban, írjuk ezt is fel az `x` és `y` irányú egységvektorok segítségével: (a Pitagorasz tétel kell hozzá, meg hogy hasonló háromszögek)
Az `AB` távolság `sqrt("0,5"^2+"0,3"^2)=sqrt(34)/10`
`v_(Ax)=v_A·"0,5"/(sqrt(34)//10)=v_A·5/sqrt(34)=50/sqrt(34)` (nem írom ki a mértékegységeket, de `m/s`)
`v_(Ay)=...=30/sqrt(34)`
Vagyis `vec(v_A)=50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y)`
A `B` pont sebessége:
`vec(v_B)=vec(v_A)+vec(ω)×vec(r_(AB))`
Az `vec(ω)` és az `vec(r_(AB))` vektoriális szorzata merőleges lesz mindkettőre. Vagyis az is a síkban lesz, de merőleges `vec(r_(AB))`-ra. Rajzolj az ábrára a `B` pontban egy merőleges egyenest szaggatottan, ami az `AB` szaggatott egyenesre merőleges. ebben az egyenesben lesz tehát a vektoriális szorzat vektora valahol (vagy fölfelé, vagy lefelé).
`vec(v_B)`-nek csak `vec(e_y)` komponense van, `vec(v_A)`-nak viszont van `vec(e_x)` komponense is. Ez azt jelenti, hogy a vektoriális szorzat `vec(e_x)` komponense ki kell hogy ejtse `vec(v_A)` vízszintes komponensét! Ez a kulcs a megoldáshoz.
... Bocs, majd folytatom, most nem érek rá pillanatnyilag. Addig is gondolkozz rajta, hogy hogyan is tovább.
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Szóval:
`vec(v_B)=vec(v_A)+vec(ω)×vec(r_(AB))`
`vec(ω)×vec(r_(AB))=vec(v_B)-vec(v_A)`
`vec(ω)×vec(r_(AB)) = b·vec(e_y)-(50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y))`
`vec(ω)×vec(r_(AB)) =-50/sqrt(34)·vec(e_x)+(b-30/sqrt(34))·vec(e_y)`
Ez a vektor merőleges az `AB` egyenesre.
Mivel `vec(r_(AB))="0,5"·vec(e_x)-"0,3"·vec(e_y)`, a rá merőleges vektor `"0,3"·vec(e_x)+"0,5"·vec(e_y)`. (Pozitív irányban forgattam el a vektort.) Ezt kell `ω`-val szorozni, amiből ez lesz:
`vec(ω)×vec(r_(AB))=ω·"0,3"·vec(e_x)+ω·"0,5"·vec(e_y)`
`ω·"0,3"·vec(e_x)+ω·"0,5"·vec(e_y)=-50/sqrt(34)·vec(e_x)+(b-30/sqrt(34))·vec(e_y)`
Ezek irányonként azonosak kell legyenek, vagyis ez a két egyenlet lesz belőlük:
`ω·"0,3"=-50/sqrt(34)`
`ω·"0,5"=b-30/sqrt(34)`
Ezekből kijön `ω` valamint `b` is. A `b` értéke nem izgalmas (nem kérdezte a feladat), csak az `ω`:
`ω=-500/(3sqrt(34))`
... a mértékegység `"rad"/s`, de nem írom oda.
A negatív szögsebesség csak azt jelenti, hogy az `vec(ω)` vektor pont ellentétes irányú, mint ahogy gondoltuk, szóval nem felénk jön ki a síkból, hanem befelé megy. Nem gond. (Mellesleg a negatív `ω` azt is jelenti, hogy ha kiszámolnánk `b` értékét, az is negatív lenne, tehát a `B` pont sebessége lefelé menő függőleges vektor.)
Kész vagyuink az első résszel, tehát a `B` pont sebességének irányából meghatároztuk az `ω` szögsebességet. Most jön a válasz a kérdésre: mi a `C` pont sebessége:
`vec(v_C)=vec(v_A)+vec(ω)×vec(r_(AC))`
Az `vec(ω)×vec(r_(AC))` vektoriális szorzat most is merőleges `vec(r_(AC))`-ra.
`vec(r_(AC))="0,5"·vec(e_x)`, az erre merőleges vektor `"0,5"·vec(e_y)` (Pozitív irányban forgattam el ezt is). Ennek az `ω`-szorosa:
`ω·"0,5"·vec(e_y)=-500/(3sqrt(34))·"0,5"·vec(e_y)=-250/(3sqrt(34))·vec(e_y)`
Így a `C` pont sebessége:
`vec(v_C)=vec(v_A)-250/(3sqrt(34))·vec(e_y)`
`vec(v_C)=50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y)-250/(3sqrt(34))·vec(e_y)`
`vec(v_C)=50/sqrt(34)·vec(e_x)-(250/(3sqrt(34))-30/sqrt(34))·vec(e_y)`
Remélem, nem számoltam el sehol...
`vec(v_B)=vec(v_A)+vec(ω)×vec(r_(AB))`
`vec(ω)×vec(r_(AB))=vec(v_B)-vec(v_A)`
`vec(ω)×vec(r_(AB)) = b·vec(e_y)-(50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y))`
`vec(ω)×vec(r_(AB)) =-50/sqrt(34)·vec(e_x)+(b-30/sqrt(34))·vec(e_y)`
Ez a vektor merőleges az `AB` egyenesre.
Mivel `vec(r_(AB))="0,5"·vec(e_x)-"0,3"·vec(e_y)`, a rá merőleges vektor `"0,3"·vec(e_x)+"0,5"·vec(e_y)`. (Pozitív irányban forgattam el a vektort.) Ezt kell `ω`-val szorozni, amiből ez lesz:
`vec(ω)×vec(r_(AB))=ω·"0,3"·vec(e_x)+ω·"0,5"·vec(e_y)`
`ω·"0,3"·vec(e_x)+ω·"0,5"·vec(e_y)=-50/sqrt(34)·vec(e_x)+(b-30/sqrt(34))·vec(e_y)`
Ezek irányonként azonosak kell legyenek, vagyis ez a két egyenlet lesz belőlük:
`ω·"0,3"=-50/sqrt(34)`
`ω·"0,5"=b-30/sqrt(34)`
Ezekből kijön `ω` valamint `b` is. A `b` értéke nem izgalmas (nem kérdezte a feladat), csak az `ω`:
`ω=-500/(3sqrt(34))`
... a mértékegység `"rad"/s`, de nem írom oda.
A negatív szögsebesség csak azt jelenti, hogy az `vec(ω)` vektor pont ellentétes irányú, mint ahogy gondoltuk, szóval nem felénk jön ki a síkból, hanem befelé megy. Nem gond. (Mellesleg a negatív `ω` azt is jelenti, hogy ha kiszámolnánk `b` értékét, az is negatív lenne, tehát a `B` pont sebessége lefelé menő függőleges vektor.)
Kész vagyuink az első résszel, tehát a `B` pont sebességének irányából meghatároztuk az `ω` szögsebességet. Most jön a válasz a kérdésre: mi a `C` pont sebessége:
`vec(v_C)=vec(v_A)+vec(ω)×vec(r_(AC))`
Az `vec(ω)×vec(r_(AC))` vektoriális szorzat most is merőleges `vec(r_(AC))`-ra.
`vec(r_(AC))="0,5"·vec(e_x)`, az erre merőleges vektor `"0,5"·vec(e_y)` (Pozitív irányban forgattam el ezt is). Ennek az `ω`-szorosa:
`ω·"0,5"·vec(e_y)=-500/(3sqrt(34))·"0,5"·vec(e_y)=-250/(3sqrt(34))·vec(e_y)`
Így a `C` pont sebessége:
`vec(v_C)=vec(v_A)-250/(3sqrt(34))·vec(e_y)`
`vec(v_C)=50/sqrt(34)·vec(e_x)+30/sqrt(34)·vec(e_y)-250/(3sqrt(34))·vec(e_y)`
`vec(v_C)=50/sqrt(34)·vec(e_x)-(250/(3sqrt(34))-30/sqrt(34))·vec(e_y)`
Remélem, nem számoltam el sehol...
0
-
Zsuzska: Mi van akkor ha az A pont sebesség vektorát kérdezik, eltolom a B pont vektorát az A pontba? Még azt nem értem, hogy a vektoriális szorzat ey komponense miért ejti ki a vA vektort? Köszönöm a megoldást és a türelmet. 6 éve 0
-
bongolo: Az A pont sebességvektora meg van adva. 6 éve 0
-
bongolo: A vektoriális szorzat nem ejti ki a vA vektort, csak a vA-nak az x komponensét. Tehát az összeg y irányú lesz. 6 éve 0
-
bongolo: Ha megrajzolod, ahogy írtam, rájössz. 6 éve 0
-
bongolo: Ezt írtam: Rajzolj az ábrára a B pontban egy merőleges egyenest szaggatottan, ami az A B szaggatott egyenesre merőleges. ebben az egyenesben lesz tehát a vektoriális szorzat vektora 6 éve 0
-
bongolo: A vektoriális szorzatnak olyan hosszúnak kell lennie, hogy annak meg vA-nak az x komponensei kiejtsék egymást. 6 éve 0
-
bongolo: Mivel vA x komponensre jobbra mutat, ezért a vekt.szorzat x komponense balra kell mutasson. Vagyis a vekt.szorzat délnyugati irányba kell menjen, nem északkeletibe, a mentén a merőleges egyenes mentén, amit berajzoltál. 6 éve 0
-
bongolo: Szólj, ha nem értesz még valamit. 6 éve 0