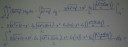Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Integrálás
 Solver
{ Elismert } kérdése
Solver
{ Elismert } kérdése
701
Az alábbi feladatban elakadtam, tudnátok segíteni? Köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
integrálszámítás, Matematika
integrálszámítás, Matematika
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Nagyon barátságtalan egy integrál ez... De a megoldásodban is van egy-két hiba. Egyrészt az első egyenlőség már rögtön nem teljesül, hiszen ha elhagyod a külső integrált, akkor nem kapod ugyanazt az eredményt. Illetve a primitívfüggvényben a logaritmus argumentumán belül nem kellene `x`-szel osztani.
Egyszerűbb a dolgod, ha kihasználod, hogy az integrandus mindkét változójában páros függvény, és ezért elég a tartomány negyedén integrálni:
`I=int_(-4)^4 int_(-4)^4 sqrt(x^2+y^2) dy dx``=``4int_0^4 int_0^4 sqrt(x^2+y^2) dy dx`
A nulla alsó határ miatt így egy fokkal szebb lesz a belső integrál eredménye:
`I=4int_0^4 (2sqrt(x^2+16)+1/2x^2ln(sqrt(x^2+16)+4)-1/2x^2lnx) dx`
Ez azért már tagonként elvégezhető, ha fáradságosan is:
`I=4 [-1/6x^3lnx+4/3x sqrt(x^2+16)+1/6x^3 ln(sqrt(x^2+16)+4)+32/3 ln(x/4+sqrt(x^2/16+1))] _0^4`
Elvégezve a behelyettesítést:
`I=256/3(sqrt(2)+ln(1+sqrt(2)))~~195.89`
Egy másik lehetőség, hogy áttérsz polárkoordinátákra:
`x=rcos varphi`
`y=rsin varphi`
`dydx=rdrd varphi`
Ekkor a `sin^2 varphi+cos^2 varphi=1` azonosságot és `r` nemnegatív voltát kihasználva az integrandus nagyon megszépül:
`I=4int int r^2 drd varphi`
Viszont sajnos a négyzet alakú tartomány poláris koordinátarendszerben elég természetellenesen írható le:
`I=4 int_0^(pi/4) int_0^(4/(cos varphi))r^2 dr d varphi+4 int_(pi/4)^(pi/2) int_0^(4/(sin varphi))r^2 dr d varphi`
Elvégezve az `r` szerinti integrálásokat:
`I=256/3 [int_0^(pi/4) 1/(cos^3 varphi) d varphi+int_(pi/4)^(pi/2) 1/(sin^3 varphi) d varphi]`
Mindkét függvénynek ugyanannyi periódusát integráljuk, ezért a két integrál egyenlő, vagyis:
`I=512/3 int_0^(pi/4) 1/(cos^3 varphi) d varphi`
Visszavezethető tehát a dolog `1/(cos^3 varphi)` integráljára. Ez sem szép, de megcsinálható. Sőt, viszonylag híres integrál: https://en.wikipedia.org/wiki/Integral_of_secant_cubed
Egyszerűbb a dolgod, ha kihasználod, hogy az integrandus mindkét változójában páros függvény, és ezért elég a tartomány negyedén integrálni:
`I=int_(-4)^4 int_(-4)^4 sqrt(x^2+y^2) dy dx``=``4int_0^4 int_0^4 sqrt(x^2+y^2) dy dx`
A nulla alsó határ miatt így egy fokkal szebb lesz a belső integrál eredménye:
`I=4int_0^4 (2sqrt(x^2+16)+1/2x^2ln(sqrt(x^2+16)+4)-1/2x^2lnx) dx`
Ez azért már tagonként elvégezhető, ha fáradságosan is:
`I=4 [-1/6x^3lnx+4/3x sqrt(x^2+16)+1/6x^3 ln(sqrt(x^2+16)+4)+32/3 ln(x/4+sqrt(x^2/16+1))] _0^4`
Elvégezve a behelyettesítést:
`I=256/3(sqrt(2)+ln(1+sqrt(2)))~~195.89`
Egy másik lehetőség, hogy áttérsz polárkoordinátákra:
`x=rcos varphi`
`y=rsin varphi`
`dydx=rdrd varphi`
Ekkor a `sin^2 varphi+cos^2 varphi=1` azonosságot és `r` nemnegatív voltát kihasználva az integrandus nagyon megszépül:
`I=4int int r^2 drd varphi`
Viszont sajnos a négyzet alakú tartomány poláris koordinátarendszerben elég természetellenesen írható le:
`I=4 int_0^(pi/4) int_0^(4/(cos varphi))r^2 dr d varphi+4 int_(pi/4)^(pi/2) int_0^(4/(sin varphi))r^2 dr d varphi`
Elvégezve az `r` szerinti integrálásokat:
`I=256/3 [int_0^(pi/4) 1/(cos^3 varphi) d varphi+int_(pi/4)^(pi/2) 1/(sin^3 varphi) d varphi]`
Mindkét függvénynek ugyanannyi periódusát integráljuk, ezért a két integrál egyenlő, vagyis:
`I=512/3 int_0^(pi/4) 1/(cos^3 varphi) d varphi`
Visszavezethető tehát a dolog `1/(cos^3 varphi)` integráljára. Ez sem szép, de megcsinálható. Sőt, viszonylag híres integrál: https://en.wikipedia.org/wiki/Integral_of_secant_cubed
2
- Még nem érkezett komment!