Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Kötél erő
 Zsuzska
kérdése
Zsuzska
kérdése
463
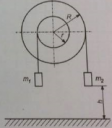
²A tárcsákra (R=0,4 m, r= 0,2 m) két kötelet csévélünk, végükön különböző tömeg függ. A tárcsák tehetetlenségi nyomatéka 2 kgm². Az m₁=25 kg tömeg álló helyzetből elindul a₁=2 m/s²gyorsulással felfelé. Mekkora az m₂ tömege? Mekkora erő feszíti a köteleket? Mennyi idő múlva éri el az m₂ tömeg a talajt, ha távolsága h= 2m?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Fizika
Válaszok
1 bongolo
{
bongolo
{  }
válasza
}
válasza
`Θ=2\ kgm^2` a tehetetlenségi nyomaték. Az olyasmi mennyiség forgómozgásnál, mint a tömeg egyenes vonalú mozgásnál:
- Egyenes vonalban az `F=m·a` képlet adja meg, hogy mekkora `F` erő kell ahhoz, hogy egy `m` tömeg gyorsuljon `a` gyorsulással. Ez a dinamika alapegyenlete.
- Forgómozgásnál formailag hasonlóan az `M=Θ·β` adja meg, hogy mekkora forgatónyomaték (`M`) kell ahhoz, hogy a `Θ` tehetetlenségi nyomatékú test forgása gyorsuljon `β` szöggyorsulással. Ez a forgómozgás alapegyenlete.
A `β` szöggyorsulás hasonló, mint az `a` gyorsulás. Ha a tárcsa `β` szöggyorsulással forog, akkor egy `r` sugarú kerületi pontja `a=r·β` gyorsulással mozog. Ezzel megegyezik az `m_1` tömegű test `a_1` gyorsulása, hisz a kötél nem nyúlik meg.
Egyébként hasonlóan kijön az is, hogy az `m_2` test gyorsulása `a_2=R·β`. Vagyis, mivel `β=a_1/r`:
`a_2=a_1·R/r` ezt már most ki tudod számolni.
Abból pedig a harmadik kérdés gyorsan megvan: álló helyzetből egy gyorsuló test által megtett út `t` idő alatt `s=1/2·a·t^2`, ezért:
`h=1/2·a_2·t^2`
Ebből kijön az idő, ami a harmadik kérdés volt.
Nézzük az első két kérdést:
Legyenek a kötélerők `F_1` és `F_2`, mindkettő lefelé irányú. Ezek forgatónyomatékai:
`M_1=F_1·r` balra lefelé forgat
`M_2=F_2·R` jobbra lefelé forgat
Ezek eredője `M_2-M_1`, jobbra lefelé forgat, hisz az `m_2` test indul el lefelé.
A tömegekre ható eredő erők:
`m_1`-re: `m_1·g-F_1`
`m_2`-re: `m_2·g-F_2`
Mivel `m_1` felfelé kezd gyorsulni, `m_1·g-F_1` negatív, szóval `F_1` a nagyobb:
`F_1-m_1·g=m_1·a_1`
`F_1=m_1·(g+a_1)`
`m_2` pedig lefelé gyorsul:
`m_2·g-F_2=m_2·a_2`
`F_2=m_2·(g-a_2)`
Az erők forgatónyomatékainak eredője által okozott szöggyorsulás:
`M_2-M_1=Θ·β`
Ebből a képletből `β`-t tudjuk: `β=a_1/r`. Persze `Θ`-t is tudjuk, meg volt adva.
`F_2·R-F_1·r=Θ·β`
Szedjük össze, milyen egyenleteket sikerült felírni:
`F_2·R-F_1·r=Θ·β`
`F_1=m_1·(g+a_1)`
`F_2=m_2·(g-a_2)`
Ez elég is, hisz csak 3 ismeretlen van benne: `F_1, F_2` és `m_2`
Fejezd be.
- Egyenes vonalban az `F=m·a` képlet adja meg, hogy mekkora `F` erő kell ahhoz, hogy egy `m` tömeg gyorsuljon `a` gyorsulással. Ez a dinamika alapegyenlete.
- Forgómozgásnál formailag hasonlóan az `M=Θ·β` adja meg, hogy mekkora forgatónyomaték (`M`) kell ahhoz, hogy a `Θ` tehetetlenségi nyomatékú test forgása gyorsuljon `β` szöggyorsulással. Ez a forgómozgás alapegyenlete.
A `β` szöggyorsulás hasonló, mint az `a` gyorsulás. Ha a tárcsa `β` szöggyorsulással forog, akkor egy `r` sugarú kerületi pontja `a=r·β` gyorsulással mozog. Ezzel megegyezik az `m_1` tömegű test `a_1` gyorsulása, hisz a kötél nem nyúlik meg.
Egyébként hasonlóan kijön az is, hogy az `m_2` test gyorsulása `a_2=R·β`. Vagyis, mivel `β=a_1/r`:
`a_2=a_1·R/r` ezt már most ki tudod számolni.
Abból pedig a harmadik kérdés gyorsan megvan: álló helyzetből egy gyorsuló test által megtett út `t` idő alatt `s=1/2·a·t^2`, ezért:
`h=1/2·a_2·t^2`
Ebből kijön az idő, ami a harmadik kérdés volt.
Nézzük az első két kérdést:
Legyenek a kötélerők `F_1` és `F_2`, mindkettő lefelé irányú. Ezek forgatónyomatékai:
`M_1=F_1·r` balra lefelé forgat
`M_2=F_2·R` jobbra lefelé forgat
Ezek eredője `M_2-M_1`, jobbra lefelé forgat, hisz az `m_2` test indul el lefelé.
A tömegekre ható eredő erők:
`m_1`-re: `m_1·g-F_1`
`m_2`-re: `m_2·g-F_2`
Mivel `m_1` felfelé kezd gyorsulni, `m_1·g-F_1` negatív, szóval `F_1` a nagyobb:
`F_1-m_1·g=m_1·a_1`
`F_1=m_1·(g+a_1)`
`m_2` pedig lefelé gyorsul:
`m_2·g-F_2=m_2·a_2`
`F_2=m_2·(g-a_2)`
Az erők forgatónyomatékainak eredője által okozott szöggyorsulás:
`M_2-M_1=Θ·β`
Ebből a képletből `β`-t tudjuk: `β=a_1/r`. Persze `Θ`-t is tudjuk, meg volt adva.
`F_2·R-F_1·r=Θ·β`
Szedjük össze, milyen egyenleteket sikerült felírni:
`F_2·R-F_1·r=Θ·β`
`F_1=m_1·(g+a_1)`
`F_2=m_2·(g-a_2)`
Ez elég is, hisz csak 3 ismeretlen van benne: `F_1, F_2` és `m_2`
Fejezd be.
0
- Még nem érkezett komment!