Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Mátrix sajátértékei és sajátvektorainak meghatározása
 MathOverflow
kérdése
MathOverflow
kérdése
535
Az általam megoldott feladat, és a gép által megoldott feladat előjeleiben különbözik. (Csatolt képekből látszik.) Ettől még jó az én megoldásom is, tehát számítanak itt igazából az előjelek, vagy nem?
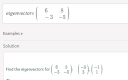
mátrix:
6 8
-3 -5
mátrix:
6 8
-3 -5
Jelenleg 1 felhasználó nézi ezt a kérdést.
mátrix, sajátérték, sajátvektor
mátrix, sajátérték, sajátvektor
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A sajátvektor olyan vektor, amit a mátrix által leírt transzformáció nem forgat el, csak skáláz. Tehát a `\mathbf{v}` vektor az `\mathbf{A}` mátrix `lambda` sajátérékhez tartozó sajátvektora, ha `\mathbf{A}\mathbf{v}= lambda \mathbf{v}`. Ennek az egyenletnek nyugodtan beszorozhatjuk mindkét oldalát egy tetszőleges `c` számmal: `\mathbf{A}*c\mathbf{v}= lambda *c\mathbf{v}`, vagyis ha egy vektor sajátvektor, akkor tetszőleges skalárszorosa is az. Tehát jó a megoldásod.
1
-
MathOverflow: Értem így már, köszönöm a segítséget! 6 éve 0