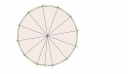
Rajzolj egy kb. szabályos 12-szöget úgy, hogy a köré írt körből indulsz ki. Szóval rajzolsz egy kört, aztán nagyjából É, K, D, Ny irányban (magyarul 90 fokonként) odaraksz a körvonalra egy-egy pöttyöt, így lesz 4 ív. Aztán mindegyik ívet harmadolod, vagyis 2 pöttyöt teszel még az ívre nagyjából azonos távolságra. Így lesz 12 pontod. Végül ezeket a pontokat összekötöd sorban. Kész a 12-szög, ami nagyjából szabályosnak is látszik.

Eddig ez volt az előkészület. Most minden csúcspontból húzz egy vonalat a kör középpontjához. Ezek mind `r` hosszúak, mindegyik sugara a köré írt körnek. Nem tudjuk, mennyi az `r`, ez a kérdés. A háromszög alapjához pedig (ami a 12-szög oldala) írd oda, hogy `a` hosszú, ezt se tudjuk még.

Lett így 12 darab egyenlő szárú háromszög. Az egyiknek rajzold be a magasságvonalát is: mivel egyenlő szárú, vagyis szimmetrikus, a magasságvonala éppen a szimmetriatengelye: felezi a háromszög alapját (`a//2`). Írd a magasságvonal mellé, hogy `m`.

Ez a magasságvonal a beírt kör sugara! Esetleg be is rajzolhatod ezt a kört, ami mindegyik kis háromszög alapját belülről érinti, de azzal már kezd kusza lenni a rajz. Én nem rajzolnám be... Nagyon sok a 12 ahhoz, hogy a beírt és körülírt kör között nagy különbség legyen, szóval nem látszódna, ne rajzold be. A mellékelt ábrán én berajzoltam, az a zöld kör, de alig látszik.

Az ábrán az ABO háromszög az, amiről eddig írtam: AB=a, AO=r, és elfelejtettem a magasság talppontját elnevezni: Legyen az az M pont, MO=m. A te rajzodba írd oda az M-et is, ami az AB oldal felezőpontja!

Szóval a beírt kör sugara az `m`, ezt tudjuk, írd a rajzod alá, hogy `m=12`.

Az O középpontnál van 12 szög, ezek együtt egy teljes kör, 360 fok. Vagyis egy ilyen csúcsnál lévő szög `360/12=30\ °`
Írd oda az egyik háromszöghöz, mondjuk ami az én ábrámon a BOC, rajzolj oda az O csúcsnál egy szög-jelző ívet, és írd oda, hogy 30°.

A magasságvonal ezt felezi, írd oda az AOM szöghöz, hogy 15°

Már majdnem kész vagyunk: Az AOM háromszög derékszögű (hisz a magasságvonal derékszögben megy oda az alaphoz), fel lehet rá írni ezt a szögfüggvényt:

Ugye egy szög koszinusza az a szög melletti befogó (m) osztva az árfogóval (r) :
`cos\ 15°=m/r`
`cos\ 15°=12/r`
`r=12/(cos\ 15°)`
Ezt számológéppel kell kiszámolni, számold ki.

A köré írt kör sugara (r) már megvan.

Oldala: Ugyanannak az AMO derékszögű háromszögnek a másik befogója `a//2`, azzal a szög szinuszát lehet felírni:
`sin\ 15°=(a//2)/r`
`a/2=r·sin\ 15°`
`a=2·r·sin\ 15°`

Ezt is számold ki számológéppel.

Leghosszabb átló: Az mondjuk az AG szakasz, ami a kör átmérője. Annak `2r` a hossza, számold ki.

Legrövidebb átló:
Az mondjuk az AC szakasz. A te ábrádra rajzod be azt a szakaszt is, nálam nincs ott.
Az a szakasz az ACO háromszög alapja. Az is egyenlő szárú háromszög, sőt, nézd meg az O-nál milyen szög van, szóval milyen az AOC szög: Az AOC háromszög két "tortacikk", vagyis az AOC szög 2·30° = 60°
Vagyis ez olyan egyenlő szárú háromszög, aminek a csúcsánál 60°-os szög van, ami szabályos (egyenlő oldalú) háromszöget jelent!
Tehát ennek minden oldala `r` hosszú, vagyis a keresett AC szakasz (a legrövidebb átló) is éppen `r`.